ベクトル
上のように定義されたベクトルは,\[\vec{a},\vec{b}\]と書きます.但し,このようなベクトルの定義はより一般的な定義の一例にしかすぎません.正確には,上で定義されたベクトルは幾何ベクトルと言われるものです.
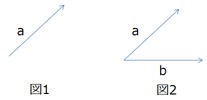
この定義がベクトルの一般的な定義になります.
ここで,線形性を持つ量をきちんと定義したものがベクトル空間,もしくは,線型空間といいます.
【定義】ベクトル空間[vector space]
集合 $V$ が以下の条件を満たしているとき $V$ を
体 $F$ 上の
ベクトル空間といいます.
ここで,$\forall u,v,w \in V$ および $\forall a,b \in K$ をとるとき,
- 結合法則:$(u+v)+w=u+(v+w)$
- 交換法則:$u+v=v+u$
- 零元の存在:$\exists 0 \in V$ が存在して$\forall v,v+0=0$
- 逆元の存在:$\forall v \in V$ に対して,$(-v) \in V$ が存在して $v+(-v)=0$ が成立する.
- 加法に対するスカラー乗法の分配律:$a(u+v)=au+av$
- 体の加法に対するスカラー乗法の分配律:$(a+b)v=av+bv$
- 体の乗法とスカラー乗法の両立条件:$a(bv)=(ab)v$
- 単位元の存在:$1v=v,1 \in K$
最初に定義したベクトル,つまり,幾何ベクトルはベクトル空間の一種です.
さきほどの一般的なベクトルの定義をきちんと書き直したものが上の定義となります.
Mathematics is the language with which God has written the universe.
