ガンマ関数
【定義】ガンマ関数[Gamma function]
実部が正となる複素数$p$について,次の積分で定義される関数\[\Gamma(z)=\int^{\infty}_{0}x^{p-1}e^{-x}\,dt\qquad(\Re{p}>0)\]をガンマ関数といいます.
.
ガンマ関数$\Gamma(p)$の性質
- $\Gamma(p+1)=p\Gamma(p)$ (詳細)
- $\Gamma(1)=1$
- $\Gamma(\frac{1}{2})=\sqrt{\pi}$
- $n$が自然数のとき以下が成り立つ.
\[\begin{eqnarray}\Gamma(\frac{1}{2})=\left\{ \begin{array}{ll}(\frac{n}{2}-1)! & (nが偶数) \\(\frac{n}{2}-1)(\frac{n}{2}-1)\cdots\frac{3}{2}\cdot\frac{1}{2}\sqrt{\pi} & (nが3以上の奇数) \\\end{array} \right.\end{eqnarray} \]
ガンマ関数とスターリングの公式
ガンマ関数をより簡単な形をした関数列の級数として近似[漸近近似;asymptotic approximation]するとスターリングの公式となります.
ガンマ関数のグラフ
ガンマ関数をグラフで描くとこうなります.
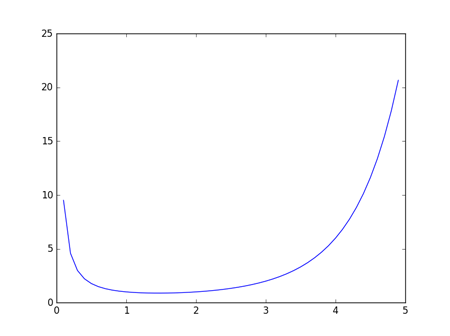
このグラフは Python で描きました.
from scipy.special import gamma
x=np.arange(0,5,1)
y=gamma(x)
plt.plot(x,y)
Vita brevis, ars longa. Omnia vincit Amor.
