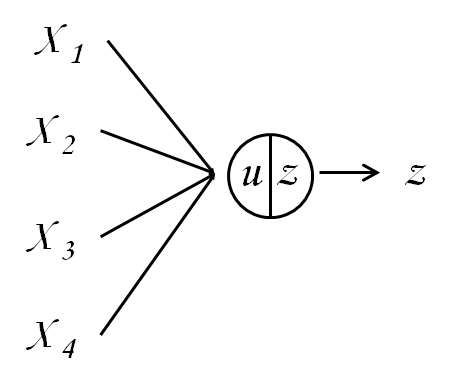
複数の入力を受け取って,1つの出力を計算する仕組みをユニットといいます.
ユニットを層状に並べて隣接する層のみで結合した構造を持っていて,情報が入力側から出力側に一方向にのみ伝わっていく構造を,順伝播型ネットワーク(feedforward neural network)といいます.
順伝播型ネットワーク(feedforward neural network)は多層パーセプトロン(multi-layer perceptron)ともいいます.
この図のユニットの場合,受け取る総入力 $u$ は,各入力 $x_{n}$ に対する重み(weight)を,$w_{n}$ として,\[u=w_{1}x_{1}+w_{2}x_{2}+w_{3}x_{3}+w_{4}x_{4}\]と表されます.
上記の式にバイアス(bias)と呼ばれる値 $b$ を加えます.\[u=w_{1}x_{1}+w_{2}x_{2}+w_{3}x_{3}+w_{4}x_{4}+b\]
ユニットの出力は,活性化関数(activation function)と呼ばれ,以下のように表されます.\[z=\varphi(w_{1}x_{1}+w_{2}x_{2}+w_{3}x_{3}+w_{4}x_{4}+b)\]
以上を入力が4つではなくて $m$ 個あるという場合を考えると,ユニットの入力関数は,\[u=\sum^{m}_{i=1}w_{i}x_{i}+b\]となり,出力関数である活性化関数は,\[z=\varphi(\sum^{m}_{i=1}w_{i}x_{i}+b)\]と表されます.
2つの層からなり,最初の層からの出力は,\[x_{1},x_{2},x_{3},x_{4}\]であり,2番目の層からの出力が\[z_{1},z_{2},z_{3}\]であるという場合を考えます.
最初のユニットの例とは異なって,$x$ が「○」で囲まれているという違いに気を付けて下さい.
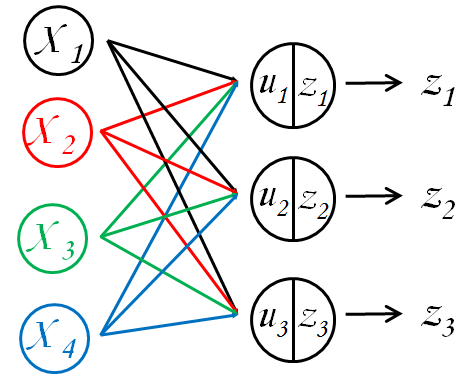
そうすると,2番目のユニットの入力関数は次のように表現されます.\[\begin{array}\s u_{1}&=w_{11}x_{1}+w_{12}x_{2}+w_{13}x_{3}+w_{14}x_{4}+b_{1}\\u_{2}&=w_{21}x_{1}+w_{22}x_{2}+w_{23}x_{3}+w_{24}x_{4}+b_{2}\\u_{3}&=w_{31}x_{1}+w_{32}x_{2}+w_{33}x_{3}+w_{34}x_{4}+b_{3}\end{array}\]
Vita brevis, ars longa. Omnia vincit Amor.