curve(sin(x),from=-2*pi,to=2*pi,type="l")
curve(cos(x),from=-2*pi,to=2*pi,type="l")
curve(sin(x),from=-2*pi,to=2*pi,type="l")
curve(cos(x),col="red",add=TRUE)
区間 $-pi \lt x \leqq \pi$ で定義された $x=0$ で不連続な関数\[\begin{eqnarray}y=\begin{cases} -\frac{\pi}{4} & (-\pi \lt x \leqq 0) \\ \frac{\pi}{4} & (0 \lt x \leqq \pi) \end{cases}\end{eqnarray}\]は,長方形の形をした波[矩形波]となります.が,この矩形波の関数をフーリエ級数展開すると,\[\begin{eqnarray}y&=&\sum^{\infty}_{k=1}\frac{\sin(2k-1)x}{2k-1}\\ &=&\sin x+\frac{\sin 3x}{3}+\frac{\sin 5x}{5}+\cdots\end{eqnarray}\]と表されます.
つまり,矩形波は正弦波の重ね合わせによって表せることになります.
par(mfrow=c(3,2))
curve(sin(x),from=-2*pi,to=2*pi,type="l")
curve(sin(x)+sin(3*x)/3,from=-2*pi,to=2*pi,type="l")
curve(sin(x)+sin(3*x)/3+sin(5*x)/5,
from=-2*pi,to=2*pi,type="l")
curve(sin(x)+sin(3*x)/3+sin(5*x)/5
+sin(7*x)/7,from=-2*pi,to=2*pi,type="l")
curve(sin(x)+sin(3*x)/3+sin(5*x)/5
+sin(7*x)/7+sin(9*x)/9,from=-2*pi,to=2*pi,type="l")
curve(sin(x)+sin(3*x)/3+sin(5*x)/5
+sin(7*x)/7+sin(9*x)/9+sin(11*x)/11,from=-2*pi,to=2*pi,type="l")
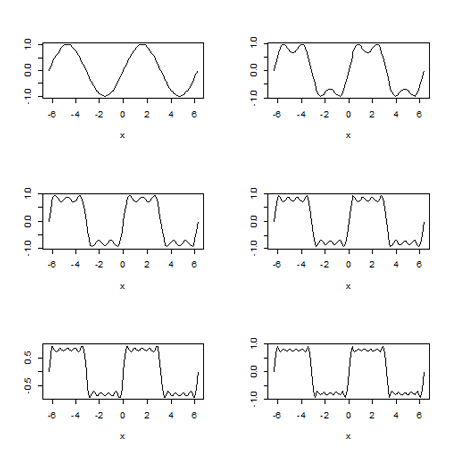
なお,矩形波の関数を正弦波の重ね合わせで表すと,端の部分にギブス[Gibbs]の現象と呼ばれるツノが出現します.このギブス[Gibbs]の現象は重ね合わせる正弦波を大きくしていったとしても消えるということはありません.
Vita brevis, ars longa. Omnia vincit Amor.