シグモイド関数

シグモイド関数は,実数の値を入力として受け取り,0から1の間の値を返す非線形関数である.この性質を利用してニューラルネットワークなどの機械学習アルゴリズムでよく使用される.

なお,シグモイド関数の特徴としては次のことが知られている.

• 入力が大きいと出力が1に近づき,入力が小さいと出力が0に近づく
• 入力が0のとき,出力は0.5になる
• 入力が0から遠く離れるほど,出力の変化が急速になる.つまり,勾配が大きくなる

ちなみに,シグモイドというのは,ギリシャ語の σῖγμα [sigma]と英語では shape や form を意味する εἶδος[eidos]に由来する.すなわち,「Sの形をした」という意味になる.また,いわゆるロジスティック関数はシグモイド関数と同義.

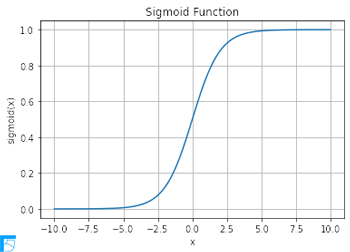
Pythonを用いてシグモイド関数を示すと次のようになる.

import numpy as np
import matplotlib.pyplot as plt

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

# xの値の範囲を定義
x = np.linspace(-10, 10, 100)  # -10から10の範囲を100個の点で均等に区切る

# シグモイド関数を計算
y = sigmoid(x)

# グラフをプロット
plt.plot(x, y)
plt.title('Sigmoid Function')
plt.xlabel('x')
plt.ylabel('sigmoid(x)')
plt.grid(True)
plt.show()

Mathematics is the language with which God has written the universe.