一般化されたシグモイド関数

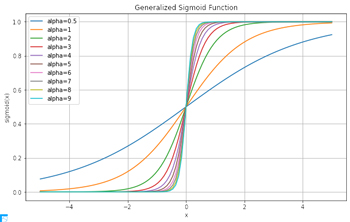
$\alpha$ の値が大きいほど一般化されたシグモイド関数の曲線は急峻になり,小さいほど緩やかになる.

このことをPythonで確認してみる.

import numpy as np
import matplotlib.pyplot as plt

# 一般化されたシグモイド関数の定義
def generalized_sigmoid(x, alpha):
    return 1 / (1 + np.exp(-alpha * x))

# xの範囲を定義
x = np.linspace(-5, 5, 100)

# αの値のリストを定義
alphas = [0.5, 1, 2, 3, 4, 5, 6, 7, 8, 9]

# グラフの描画
plt.figure(figsize=(10, 6))
for alpha in alphas:
    y = generalized_sigmoid(x, alpha)
    plt.plot(x, y, label=f'alpha={alpha}')

plt.title('Generalized Sigmoid Function')
plt.xlabel('x')
plt.ylabel('sigmoid(x)')
plt.legend()
plt.grid(True)
plt.show()

Mathematics is the language with which God has written the universe.