ヒンジ損失関数

ヒンジ損失関数は,正解ラベルと予測値の内積を計算し,その結果から 1 を引いた値と 0 とを比較し大きい方を選択する.正解ラベルと予測値が一致する場合に損失が 0 となり,一致しない場合には予測が間違っている程度に応じて損失が増加する.

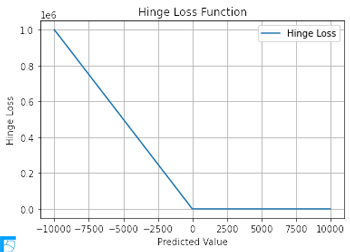
予測値を 100 で一定として,ヒンジ損失関数をPythonで実装すると次のようになる.

import numpy as np
import matplotlib.pyplot as plt

# ヒンジ損失関数の定義
def hinge_loss(y_true, y_pred):
    return np.maximum(0, 1 - y_true * y_pred)

# true value
true_value = 100

# 予測値の範囲を設定
y_pred_range = np.linspace(-10000, 10000, 1000)

# ヒンジ損失を計算
loss_values = [hinge_loss(true_value, y_pred) for y_pred in y_pred_range]

# グラフの描画
plt.plot(y_pred_range, loss_values, label='Hinge Loss')
plt.xlabel('Predicted Value')
plt.ylabel('Hinge Loss')
plt.title('Hinge Loss Function')
plt.grid(True)
plt.legend()
plt.show()

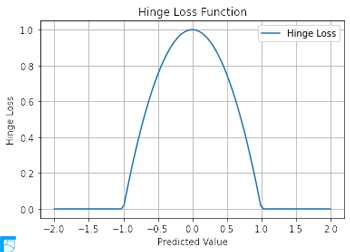
次に,y_true_range と y_pred_range を,それぞれ真のラベルと予測値の範囲を示すものとする.そして,真のラベルと予測値のそれぞれに,-2 から 2 までの範囲を100個の等間隔に区切り, -2, -1.96, -1.92, ..., 2 という値を代入する.それを zip（ ）関数を使って,複数のイテラブルから要素を取り出してタプルのペアを生成する.その上で,ヒンジ損失関数を描くと次のようになる.

import numpy as np
import matplotlib.pyplot as plt

# ヒンジ損失関数の定義
def hinge_loss(y_true, y_pred):
    return np.maximum(0, 1 - y_true * y_pred)

# y_trueとy_predの範囲を設定
y_true_range = np.linspace(-2, 2, 100)
y_pred_range = np.linspace(-2, 2, 100)

# ヒンジ損失を計算
loss_values = [hinge_loss(y_true, y_pred) for y_true, y_pred in zip(y_true_range, y_pred_range)]

# グラフの描画
plt.plot(y_pred_range, loss_values, label='Hinge Loss')
plt.xlabel('Predicted Value')
plt.ylabel('Hinge Loss')
plt.title('Hinge Loss Function')
plt.grid(True)
plt.legend()
plt.show()

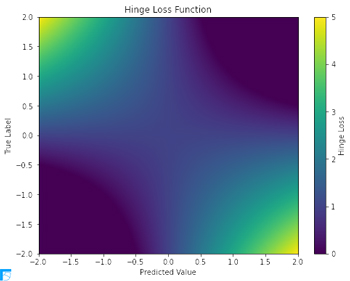
次に,真のラベルと予測値の範囲を示しものとする.そして,それぞれ,-2 から 2 までの範囲を,今度は400個の等間隔に区切り,同様にして値を代入し,ヒートマップを描く.

import numpy as np
import matplotlib.pyplot as plt

# ヒンジ損失関数の定義
def hinge_loss(y_true, y_pred):
    loss = np.maximum(0, 1 - y_true * y_pred)
    return loss

# 正解ラベルと予測値の範囲を定義
y_true_range = np.linspace(-2, 2, 400)
y_pred_range = np.linspace(-2, 2, 400)

# ヒンジ損失を計算
loss_values = np.zeros((len(y_true_range), len(y_pred_range)))
for i, y_true in enumerate(y_true_range):
    for j, y_pred in enumerate(y_pred_range):
        loss_values[i, j] = hinge_loss(y_true, y_pred)
        
# プロット
plt.figure(figsize=(8, 6))
plt.imshow(loss_values, extent=[-2, 2, -2, 2], cmap='viridis', origin='lower', aspect='auto')
plt.colorbar(label='Hinge Loss')
plt.xlabel('Predicted Value')
plt.ylabel('True Label')
plt.title('Hinge Loss Function')
plt.grid(False)
plt.show()

Mathematics is the language with which God has written the universe.