最小二乗誤差

最小自乗誤差は平均自乗誤差とも呼ばれる.

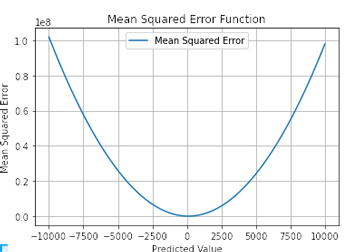
与えられたデータセット[実際の値]を 100 とし,予測値は -10,000 から 10,000 に均一に分布するとした場合の最小二乗誤差をPythonで描くと次のようになる.

import numpy as np
import matplotlib.pyplot as plt

# 最小二乗誤差関数の定義
def mean_squared_error(y_true, y_pred):
    return (y_true - y_pred)**2

# true value
true_value = 100

# 予測値の範囲を設定
y_pred_range = np.linspace(-10000, 10000, 1000)

# 最小二乗誤差を計算
loss_values = [mean_squared_error(true_value, y_pred) for y_pred in y_pred_range]

# グラフの描画
plt.plot(y_pred_range, loss_values, label='Mean Squared Error')
plt.xlabel('Predicted Value')
plt.ylabel('Mean Squared Error')
plt.title('Mean Squared Error Function')
plt.grid(True)
plt.legend()
plt.show()

Mathematics is the language with which God has written the universe.