平均絶対誤差

定義：

$y_i$ を真の値とし,$\hat{y}_i$ を対応する予測値としたとき,与えられたデータセットが $\{ (x_i, y_i) \}_{i=1}^{n}$ である場合,平均絶対誤差[Mean Absolute Error, MAE]は次のように定義される.\[ \frac{1}{n} \sum_{i=1}^{n} |y_i - \hat{y}_i|\]

平均絶対誤差[MAE]の式から $\frac{1}{n}$ を外すと,L1ノルム[マンハッタン距離]の式と同じ式となる.このことから,平均絶対誤差[MAE]は,L1損失[L1 Loss]ともL1ノルム損失[L1-norm Loss]とも呼ばれる.

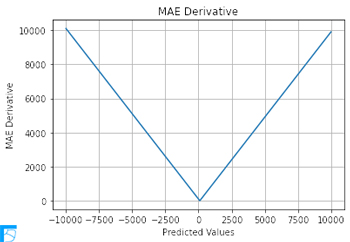
ここで,真の値 y_true を 100 で一定とし,予測値 y_pred を -10,000 から 10,000 まで一定の割合で変化させたときの平均絶対誤差[MAE]の微分値をPythonで描く.

import numpy as np
import matplotlib.pyplot as plt

# 平均絶対誤差 (MAE) を計算する関数
def mae(y_true, y_pred):
    return np.mean(np.abs(y_true - y_pred))

# MAEの微分を計算する関数
def mae_derivative(y_true, y_pred):
    return np.where(y_true > y_pred, 1, -1) * (y_true - y_pred)

# 真の値と予測値の設定
y_true = 100
# -10,000から10,000まで一定の割合で変化
y_pred_range = np.linspace(-10000, 10000, 1000)  

# MAEの微分の計算
mae_deriv_values = mae_derivative(y_true, y_pred_range)

# グラフの描画
plt.plot(y_pred_range, mae_deriv_values)
plt.xlabel('Predicted Values')
plt.ylabel('MAE Derivative')
plt.title('MAE Derivative')
plt.grid(True)
plt.show()

ここで,mae_derivative（y_true, y_pred）関数は,真の値 y_true と予測値 y_pred からMAEの微分を計算している.その中で,NumPy の np.where関数を使用して条件に応じて 1 または -1 を割り当て,そこに予測誤差を掛けている.

Mathematics is the language with which God has written the universe.

view関数最小二乗誤差ヒンジ損失関数一般化されたシグモイド関数シグモイド関数 XORゲート