Huber損失関数

Huber損失関数は,ロバスト回帰で利用される損失関数の一つ.平均二乗誤差[MSE]よりも外れ値に敏感でないことを特徴としている.Peter J. Huberにより発表されたことからHuber損失関数と呼ばれる.

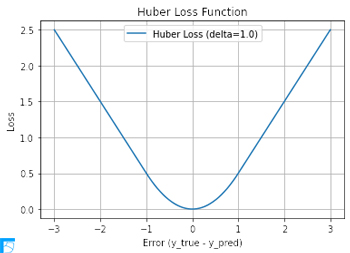
Huber Loss関数をPythonで描画する.

import numpy as np
import matplotlib.pyplot as plt

def huber_loss(y_true, y_pred, delta):
    error = np.abs(y_true - y_pred)
    quadratic_loss = 0.5 * error**2
    linear_loss = delta * (error - 0.5 * delta)
    return np.where(error <= delta, quadratic_loss, linear_loss)

# パラメータの設定
delta = 1.0
# 真の値
y_true = np.linspace(-3, 3, 100)  
# 予測値
y_pred = np.zeros_like(y_true)    

# Huber Loss関数の計算
loss = huber_loss(y_true, y_pred, delta)

# グラフの描画
plt.plot(y_true, loss, label='Huber Loss (delta={})'.format(delta))
plt.title('Huber Loss Function')
plt.xlabel('Error (y_true - y_pred)')
plt.ylabel('Loss')
plt.legend()
plt.grid(True)
plt.show()

参考文献

Huber, Peter J.（1964）. “Robust Estimation of a Location Parameter”. Annals of Statistics 53（1）: 73–101.

Mathematics is the language with which God has written the universe.