ポワソン損失関数

定義：

真の値が

$y$ が非負の整数値である場合,ポアソン損失

$L(y, \hat{y})$ は,次のように定義される.

L (y, \hat{y}) = \hat{y} - y \cdot \log (\hat{y} + ϵ)

ここで,ここで,

$\hat{y}$ は予測値,

$\epsilon$ は安定性のために追加される小さな定数である.

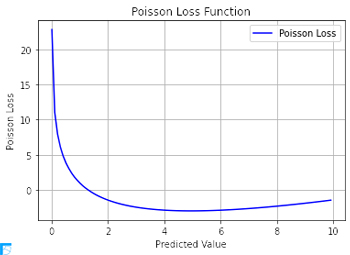
ポアソン損失をPythonで描画すると次のようになる.

import numpy as np
import matplotlib.pyplot as plt
 
# ポアソン損失関数の定義
def poisson_loss(y_true, y_pred):
    return np.mean(y_pred - y_true * np.log(y_pred + 1e-9))
 
# 真の値と予測値の範囲を設定
y_true = np.arange(0, 10, 0.1)
y_pred_range = np.arange(0.01, 10, 0.1)
 
# ポアソン損失の計算
loss_values = [poisson_loss(y_true, y_pred) for y_pred in y_pred_range]
 
# グラフの描画
plt.plot(y_pred_range, loss_values, label='Poisson Loss', color='blue')
plt.xlabel('Predicted Value')
plt.ylabel('Poisson Loss')
plt.title('Poisson Loss Function')
plt.legend()
plt.grid(True)
plt.show()

Mathematics is the language with which God has written the universe.

仮想回線 Huber損失関数イテラブル zip（）関数平均絶対誤差最小二乗誤差