p値関数

• $H_{0}$：帰無仮説[null hypothesis]
• $H_{1}$：対立仮説[alternative hypothesis]
• $T$：検定統計量[test statistic]

としたとき,p値は以下のように計算される.

• 帰無仮説が正しいと仮定して,検定統計量 $T$ 以上の値が得られる確率を計算.
• 両側検定の場合には,帰無仮説よりも $T$ が極端な値[またはそれ以上の値]が得られる確率を計算.

すなわち,観測された統計量 $t_{observed}$ よりも極端な値が得られる確率は,確率密度関数を積分することで求められる.\[\text{p-value} = P(T \geq t_{\text{observed}} | H_0) = \int_{t_{\text{observed}}}^{\infty} f(t|H_0) \, dt\]ここで,$f(t|H_{0})$ は帰無仮説 $H_{0}$ の下で検定統計量 $T$ の確率密度関数[PDF]を表す.

R に "Student’s Sleep Data" というデータセットが同梱されている.このデータセットは被験者が薬を服用した場合と服用しなかった場合の睡眠時間の差を調査したデータであり,次のようになっている.

   rownames  extra  group  ID
0         1    0.7      1   1
1         2   -1.6      1   2
2         3   -0.2      1   3
3         4   -1.2      1   4
4         5   -0.1      1   5

ここで,

• ID: 各被験者の識別子や番号
• Group: 薬を服用した群[Treatment]と服用しなかった群[Control]のいずれかを示す変数.
• Extra: 薬を服用した場合と服用しなかった場合の睡眠時間の差を示す変数.この値は睡眠時間の変化を表す.

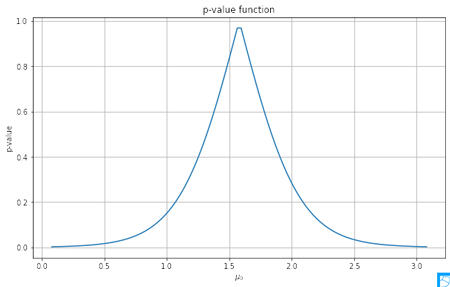
このデータを用いて,群間の睡眠時間の差が $0$ であるという帰無仮説を設定する.つまり,\[\mu_{0}=0\]と仮定し,標本データから,1標本のt検定におけるt統計量,すなわち,\[t = \frac{\bar{x} - \mu_0}{s / \sqrt{n}}\]で計算される.これを用いて,p値関数をpythonで描画する.

import numpy as np
import pandas as pd
from scipy.stats import t, ttest_1samp
import matplotlib.pyplot as plt

def prop_t(mu, xbar=0, se=1, df=1, alternative="two.sided"):
    """
    Compute the t-statistic and p-value for a hypothesis test about the mean.
    
    Parameters:
        mu (float): 仮説の母集団平均.
        xbar (float, optional): 標本平均. デフォルトは 0.
        se (float, optional): 標本平均の標準誤差. デフォルトは 1.
        df (int, optional): t分布の自由度. デフォルトは 1.
        alternative (str, optional): 対立仮説, "two.sided", "less", or "greater" を設定. デフォルトは "two.sided".
    
    Returns:
        float: 仮説検定における p値 .
    """
    if alternative not in ["two.sided", "less", "greater"]:
        raise ValueError("alternative must be either 'two.sided', 'less', or 'greater'.")
    
    v = (xbar - mu) / se
    
    if alternative == "two.sided":
        p0 = 2 * t.sf(abs(v), df)
    elif alternative == "less":
        p0 = t.cdf(v, df)
    elif alternative == "greater":
        p0 = t.sf(v, df)
    
    return p0

# Load sleep dataset
sleep = pd.read_csv("https://vincentarelbundock.github.io/Rdatasets/csv/datasets/sleep.csv", index_col=0)



# Statistical analysis
sleep2 = sleep.pivot(index='ID', columns='group', values='extra')
x_d = sleep2[2] - sleep2[1]
res0 = ttest_1samp(x_d, 0)

xbar = np.mean(x_d)
se = np.std(x_d) / np.sqrt(len(x_d))

len_mu = 100
mu0 = np.linspace(xbar - 1.5, xbar + 1.5, len_mu)
res = [ttest_1samp(x_d, mu) for mu in mu0]

alpha = np.linspace(0, 0.5, len_mu)

resdf = pd.DataFrame({
    'time_dummy': np.arange(1, len_mu + 1),
    'p_dummy': np.concatenate([np.flip(np.arange(1, len_mu//2 + 1)), np.arange(1, len_mu//2 + 1)]),
    'mu0': mu0,
    'stat': [r.statistic for r in res],
    'pval': [r.pvalue for r in res]
})

# Calculate confidence interval
ci = t.ppf(0.975, len(x_d)-1) * se

# Plot results


plt.figure(figsize=(10, 6))
plt.plot(mu0, [prop_t(mu, xbar=xbar, se=se, df=len(x_d)-1) for mu in mu0], linestyle='-')
plt.xlabel('$\mu_0$')
plt.ylabel('p-value')
plt.title('p-value function')
plt.grid(True)
plt.show()

Mathematics is the language with which God has written the universe.