t分布の正規分布近似

t分布*の確率密度関数は確率変数を $x$, $n$ を自由度としたとき,\[{ t }_{ n }(x)=\frac { 1 }{ \sqrt { n } B(\frac { n }{ 2 } ,\frac { 1 }{ 2 } ) } { \left(\frac { { x }^{ 2 } }{ n } +1\right) }^{ -\frac { n+1 }{ 2 } }\]と表される.

ここで,自由度 $n$ が大きくなるに従って,t分布が正規分布に近づくことを示す.

まず,二項分布とポアソン分布の関係*から,\[\lim_{n\to\infty}\left(1-\frac{\mu}{n}\right)^{n}=\lim_{n\to\infty}\left(1-\frac{\mu}{n}\right)^{-\frac{n}{\mu} \times (-\mu)}=e^{-\mu}\]であるので,これを用いると,t分布*の確率密度関数の四角く囲った部分に適用する.\[{ t }_{ n }(x)=\frac { 1 }{ \sqrt { n } B(\frac { n }{ 2 } ,\frac { 1 }{ 2 } ) } \boxed{\color{red}{\left(\frac { { x }^{ 2 } }{ n } +1\right)^{ -\frac { n+1 }{ 2 }}}}\]すると,\[\begin{eqnarray}\boxed{\color{red}{\left(\frac { { x }^{ 2 } }{ n } +1\right)^{ -\frac { n+1 }{ 2 }}}}&=&\left(1+\frac{x^{2}}{n}\right)^{-\frac{x^{2}}{2}\frac{n}{x^{2}}}\left(1+\frac{x^{2}}{n}\right)^{-\frac{1}{2}}\\&\rightarrow&e^{-\frac{x^{2}}{2}}\end{eqnarray} \]となる.

次に,t分布*の確率密度関数の前半の部分について考える.\[{ t }_{ n }(x)=\boxed{\color{red}{\frac { 1 }{ \sqrt { n } B \left(\frac { n }{ 2 } ,\frac { 1 }{ 2 } \right) }}} { \left(\frac { { x }^{ 2 } }{ n } +1\right) }^{ -\frac { n+1 }{ 2 } }\]ここで,\[\boxed{\color{red}{\frac { 1 }{ \sqrt { n } B \left(\frac { n }{ 2 } ,\frac { 1 }{ 2 } \right) }}}=\frac { 1 }{ \sqrt { n }} \frac{\Gamma\left(\frac{1}{2}+\frac{n}{2}\right)}{\Gamma\left(\frac{1}{2}\right)\Gamma\left(\frac{n}{2}\right)}\]である.なお,\[\Gamma\left(\frac{1}{2}\right)=\sqrt{\pi}\]であるから,結局,\[\frac { 1 }{ \sqrt { n }} \frac{\Gamma\left(\frac{1}{2}+\frac{n}{2}\right)}{\Gamma\left(\frac{1}{2}\right)\Gamma\left(\frac{n}{2}\right)}=\frac { 1 }{ \sqrt { n }\sqrt { \pi }} \frac{\Gamma\left(\frac{1}{2}+\frac{n}{2}\right)}{\Gamma\left(\frac{n}{2}\right)}\]について考えていくことになる.これが,自由度 $\nu$ が大きくなると,標準正規分布 $N(0,1)$ の確率密度関数になる.このことを,スターリングの公式*[Stirling's formula]\[\Gamma(N) \simeq \sqrt{2 \pi N}(\frac{N}{e})^{N}\]を用いて示していく.先ほどの式を整理すると,\[\frac { 1 }{ \sqrt { n }\sqrt { \pi }} \frac{\Gamma\left(\frac{1}{2}+\frac{n}{2}\right)}{\Gamma\left(\frac{n}{2}\right)}=\frac{(\frac{1}{e})^{\frac{n+1}{1}} \cdot \sqrt{2\pi \cdot \frac{n+1}{2}} \cdot \left(\frac{n+1}{2}\right)^{\frac{n+1}{2}}}{\sqrt{n\pi} \cdot (\frac{1}{e})^{\frac{n}{2}} \cdot \sqrt{2\pi\frac{n}{2}} \cdot \left(\frac{n}{2}\right)^{\frac{n}{2}}}\]さらに式を変形して整理していく,\[\begin{eqnarray}\frac{\left(\frac{1}{e}\right)^{\frac{n+1}{2}} \cdot \sqrt{2\pi} \cdot \frac{n+1}{2} \cdot \left(\frac{n+1}{2}\right)^{\frac{n+1}{2}}}{\sqrt{n\pi} \cdot \left(\frac{1}{e}\right)^{\frac{n}{2}} \cdot \sqrt{2\pi\frac{n}{2}} \cdot \left(\frac{n}{2}\right)^{\frac{n}{2}}}&=&\left(\frac{1}{e}\right)^{\frac{n+1}{2}-\frac{n}{2}} \cdot \frac{1}{\sqrt{n\pi}} \cdot \frac{\sqrt{\pi \cdot (n+1)}}{\pi \cdot \left(\frac{n}{2}\right)} \cdot \frac{\left(\frac{n+1}{2}\right)^{\frac{n+1}{2}}}{\left(\frac{n}{2}\right)^{\frac{n}{2}}}\\&=&\frac{1}{\sqrt{n \pi}} \cdot \left(\frac{1}{e}\right)^{\frac{1}{2}} \cdot \sqrt{\frac{n+1}{n}} \cdot \left(\frac{n+1}{n}\right)^{\frac{n+1}{2}} \cdot \left(\frac{n}{2}\right)^{-\frac{n}{2}}\\&=&\frac{1}{\sqrt{n \pi}} \cdot \left(\frac{1}{e}\right)^{\frac{1}{2}} \cdot \left(\frac{1}{n}\right)^{\frac{1}{2}} \cdot (n+1)^{\frac{1}{2}} \cdot \left(\frac{1}{2}\right)^{\frac{n+1}{2}} \cdot (n+1)^{\frac{n+1}{2}} \cdot \left(\frac{1}{2}\right)^{-\frac{n}{2}} \cdot n^{-\frac{n}{2}}\\&=&\frac{1}{\sqrt{n \pi}} \cdot \left(\frac{1}{e}\right)^{\frac{1}{2}} \cdot \left(\frac{1}{n}\right)^{\frac{1}{2}} \cdot \left(\frac{1}{2}\right)^{\frac{n+1}{2}} \cdot \left(\frac{1}{2}\right)^{-\frac{n}{2}} \cdot (n+1)^{\frac{1}{2}} \cdot (n+1)^{\frac{n+1}{2}} \cdot n^{-\frac{n}{2}}\\&=&\frac{1}{\sqrt{n \pi}} \cdot \left(\frac{1}{e}\right)^{\frac{1}{2}} \cdot n^{-\frac{1}{2}} \cdot n^{-\frac{n}{2}} \cdot (n+1)^{\frac{1}{2}} \cdot (n+1)^{\frac{n+1}{2}} \cdot \left(\frac{1}{2}\right)^{\frac{1}{2}}\\&=&n^{-\frac{1}{2}} \cdot \pi^{-\frac{1}{2}} \cdot \left(\frac{1}{2}\right)^{\frac{1}{2}} \cdot \left(\frac{1}{e}\right)^{\frac{1}{2}} \cdot n^{-\frac{n+1}{2}} \cdot (n+1)^{\frac{n+2}{2}}\\&=&\frac{1}{\sqrt{2\pi}} \cdot \left(\frac{1}{e}\right)^{\frac{1}{2}} \cdot n^{-\frac{n+2}{2}} \cdot (n+1)^{\frac{n+2}{2}}\\&=&\frac{1}{\sqrt{2\pi}} \cdot \left(\frac{1}{e}\right)^{\frac{1}{2}} \cdot \left(\frac{n+1}{n}\right)^{\frac{n+2}{2}}\end{eqnarray}\]ここで,再び二項分布とポアソン分布の関係から, $n \rightarrow \infty$ となるとき,\[\left(\frac{n-1}{n-2}\right)^{\frac{n-1}{2}}=\left(1+\frac{1}{n-2}\right)^{(n-2) \cdot 2 +\frac{1}{2}} \rightarrow e^{\frac{1}{2}}\]となる.従って,先の式は結局,\[\frac{1}{\sqrt{2\pi}} \cdot \left(\frac{1}{e}\right)^{\frac{1}{2}} \cdot \left(\frac{n+1}{n}\right)^{\frac{n+2}{2}} \rightarrow \frac{1}{\sqrt{2\pi}}\]となる.すなわち,$n$ が十分に大きくなると,t分布は正規分布に近似される.$\square$

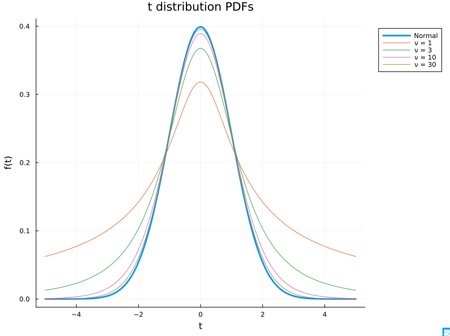
次に,Juliaを使って,自由度 $\nu$ が大きくなると,t分布は標準正規分布 $N(0,1)$ に近づくことを示す.

import Pkg
Pkg.add("Plots")
using Plots

Pkg.add("Distributions")
using Distributions
import Distributions: pdf

Pkg.add("StatsFuns")
using StatsFuns

# t分布のPDF
function tpdf(t, ν)
    γ = StatsFuns.gamma((ν+1)/2) / sqrt(ν*pi) 
        / StatsFuns.gamma(ν/2)
    γ * (1 + t^2/ν)^(-ν/2)
end

# 標準正規分布のPDF
function normalpdf(t)
    return pdf(Normal(0, 1), t)
end

ν_values = [1, 3, 10, 30]
# x範囲を拡張し,より滑らかに描画
ts = -5:0.01:5  

# 1x1のレイアウト,凡例を右上に配置
plot(legend=:outertopright)  

# 正規分布を太線で描画
plot!(ts, [normalpdf(t) for t in ts], label="Normal", lw=3, 
xlabel="t", ylabel="f(t)", title="t distribution PDFs")  

for ν in ν_values
    plot!(ts, [tpdf(t, ν) for t in ts], label="ν = $ν")
end

# プロットのサイズを設定
plot!(size=(800, 600))

Mathematics is the language with which God has written the universe.