離散一様分布

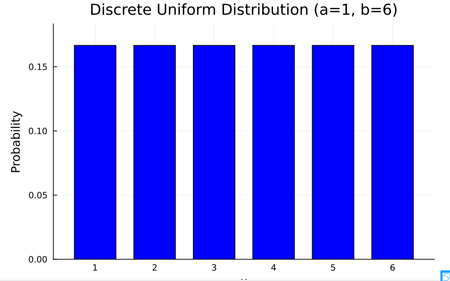
離散一様分布をJuliaで描画する.

using Plots
using StatsBase

# パラメータ設定
n = 10  # サンプル数
a = 1   # 最小値
b = 6   # 最大値

# 離散一様分布の確率質量関数
x = a:b
p = fill(1/(b-a+1), length(x))

# グラフ描画
bar(x, p, 
    xlabel="x", 
    ylabel="Probability", 
    title="Discrete Uniform Distribution (a=$a, b=$b)",
    legend=false,
    bar_width=0.7,
    ylim=(0, 1.1*maximum(p)),
    color=:blue)

離散一様分布の期待値

離散確率変数 $X$ の期待値は以下のように定義される.\[E[X] = \sum_{x} x \cdot P(X = x)\]離散一様分布の確率質量関数は,\[P(X = x) = \frac{1}{b - a + 1} \text{ for } x = a, a+1, \ldots, b\]期待値の計算をする.\[\begin{eqnarray} E[X] &=& \sum_{x=a}^{b} x \cdot P(X = x) \\ &=& \sum_{x=a}^{b} x \cdot \frac{1}{b - a + 1} \\ &=& \frac{1}{b - a + 1} \sum_{x=a}^{b} x \end{eqnarray}\]ここで,等差数列の和の公式を適用する.等差数列 $a, a+1, \ldots, b$ の和は,\[\sum_{x=a}^{b} x = \frac{(a + b)(b - a + 1)}{2}\]となる.従って,\[\begin{eqnarray}E[X] &=& \frac{1}{b - a + 1} \cdot \frac{(a + b)(b - a + 1)}{2} \\ &=& \frac{a + b}{2}\end{eqnarray}\]よって,期待値は, \[E[X] = \frac{a + b}{2}\]

この結果は,分布の中央値（最小値 $a$ と最大値 $b$ の平均）を表している.離散一様分布では,すべての値が等確率で発生するため,期待値はちょうど中央の値となる.

離散一様分布の分散

分散の定義は,\[Var(X) = E[(X - E[X])^2] = E[X^2] - (E[X])^2\]である.ここで,離散一様分布の期待値は,\[E[X] = \frac{a + b}{2}\]であることから,$E[X^2]$ は,\[\begin{eqnarray}E[X^2] &=& \sum_{x=a}^{b} x^2 \cdot P(X = x) \\ &=& \frac{1}{b - a + 1} \sum_{x=a}^{b} x^2\end{eqnarray}\]二乗の和の公式を適用すると,\[\sum_{x=a}^{b} x^2 = \frac{(b-a+1)(a+b)(2b+2a+1)}{6}\]となることから,\[\begin{eqnarray}E[X^2] &=& \frac{1}{b - a + 1} \cdot \frac{(b-a+1)(a+b)(2b+2a+1)}{6} \\ &=& \frac{(a+b)(2b+2a+1)}{6}\end{eqnarray}\]従って,\[\begin{eqnarray}Var(X) &= E[X^2] - (E[X])^2 \\ &=& \frac{(a+b)(2b+2a+1)}{6} - \left(\frac{a + b}{2}\right)^2 \\ &=& \frac{(a+b)(2b+2a+1)}{6} - \frac{(a+b)^2}{4} \\ &=& \frac{2(a+b)(2b+2a+1) - 3(a+b)^2}{12} \\ &=& \frac{(a+b)(4b+4a+2 - 3a - 3b)}{12} \\ &=& \frac{(a+b)(b-a+2)}{12}\end{eqnarray}\]整理すると,\[\begin{eqnarray}Var(X) &=& \frac{(a+b)(b-a+2)}{12} \\ &=& \frac{(b+a)(b-a) + 2(b+a)}{12} \\ &=& \frac{b^2 - a^2 + 2b + 2a}{12} \\ &=& \frac{(b-a+1)(b+a+1)}{12} \\ &=& \frac{(b-a+1)^2 - 1}{12}\end{eqnarray}\]すなわち,離散一様分布の分散は,\[Var(X) = \frac{(b - a + 1)^2 - 1}{12}\]となる.

離散一様分布のモーメント母関数

モーメント母関数の定義は,\[M_X(t) = E[e^{tX}] = \sum_{x} e^{tx} \cdot P(X = x)\]である.ここで,離散一様分布の確率質量関数は以下のように表される.\[P(X = x) = \frac{1}{b - a + 1} \text{ for } x = a, a+1, \ldots, b\]これを用いて,モーメント母関数を計算する.\[\begin{eqnarray}M_X(t) &=& \sum_{x=a}^{b} e^{tx} \cdot P(X = x) \\ &=& \frac{1}{b - a + 1} \sum_{x=a}^{b} e^{tx} \\ &=& \frac{1}{b - a + 1} (e^{at} + e^{(a+1)t} + \cdots + e^{bt})\end{eqnarray}\]ところで,等比数列 $r, r^2, \ldots, r^n$ の和は, \[\frac{r(1-r^n)}{1-r} (r \neq 1)\]となる.ここで, $r = e^t$ とし, $n = b - a + 1$ とすると,\[\begin{eqnarray}\sum_{x=a}^{b} e^{tx} &=& e^{at} \cdot \frac{e^t(1-e^{(b-a+1)t})}{1-e^t} \\ &=& \frac{e^{at}(e^t - e^{(b-a+2)t})}{1-e^t} \\ &=& \frac{e^{(a+1)t} - e^{(b+1)t}}{1-e^t}\end{eqnarray}\]続けると,\[\begin{eqnarray}M_X(t) &=& \frac{1}{b - a + 1} \cdot \frac{e^{(a+1)t} - e^{(b+1)t}}{1-e^t} \\ &=& \frac{e^{(a+1)t} - e^{(b+1)t}}{(b - a + 1)(1-e^t)}\end{eqnarray}\]整理すると,\[\begin{eqnarray}M_X(t) &=& \frac{e^{(a+1)t} - e^{(b+1)t}}{(b - a + 1)(1-e^t)} \\ &=& \frac{e^t(e^{at} - e^{(b+1)t})}{(b - a + 1)(1-e^t)} \\ &=& \frac{e^{at} - e^{(b+1)t}}{(b - a + 1)(1 - e^t)}\end{eqnarray}\]つまり,離散一様分布のモーメント母関数は,\[M_X(t) = \frac{e^{at} - e^{(b+1)t}}{(b - a + 1)(1 - e^t)}\]となる.

Mathematics is the language with which God has written the universe.