ガンマ関数

ガンマ関数はオイラーによって,階乗の複素数への拡張[複素階乗]として考案された.ガンマ関数は第二種オイラー積分[Euler integral of the second kind]ともいう.

ところで,\[\begin{eqnarray}\Gamma(1)&=&\int_{0}^{\infty}t^{1-1}e^{-t}dt\\&=&\int_{0}^{\infty}e^{-t}dt\\&=&\lbrack -e^{-t} \rbrack_{0}^{\infty}\\&=&1 \end{eqnarray}\]また,\[\begin{eqnarray}\Gamma(z+1)&=&\int_{0}^{\infty}t^{z+1-1}e^{-t}dt\\&=&\int_{0}^{\infty}t^{z}(-e^{-t})'dt\\&=&\lbrack -t^{ze^{-t}} \rbrack_{0}^{\infty}+z\int_{0}^{\infty}t^{z-1}e^{-t}dt\\&=&z\Gamma(z)\end{eqnarray}\]となることから,\[\Gamma(n+1)=n!\]が成り立つ.

ガンマ関数$\Gamma(p)$の性質

• $\Gamma(p+1)=p\Gamma(p)$　(詳細)
• $\Gamma(1)=1$
• $\Gamma(\frac{1}{2})=\sqrt{\pi}$
• $n$が自然数のとき以下が成り立つ．

ガンマ関数とスターリングの公式

ガンマ関数をより簡単な形をした関数列の級数として近似[漸近近似;asymptotic approximation]するとスターリングの公式となります．

ガンマ関数のグラフ

ガンマ関数をグラフで描くとこうなります．

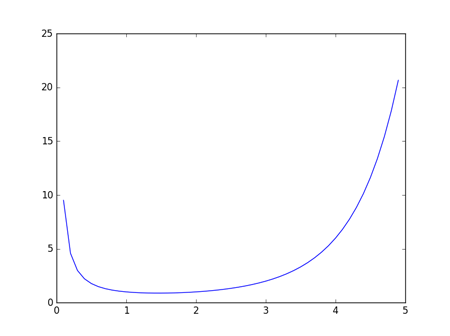
このグラフは Python で描きました．

from scipy.special import gamma
x=np.arange(0,5,1)
y=gamma(x)
plt.plot(x,y)

Mathematics is the language with which God has written the universe.