ビオ・サバールの法則

ビオ・サバールの法則[Biot-Savart law]

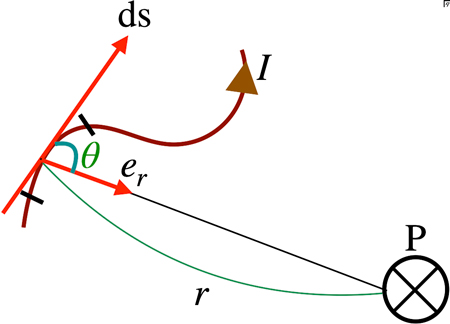
微小な長さ $\Delta l$[m] の電流要素 $I\rm{ds}$[A] によって,そこから $r$[m] の距離だけ離れている位置に作られる磁界 $\rm{d}H$ は,$\textbf{r}$方向の単位ベクトル $\textbf{e}_{r}$ とすると,\[\rm{d}\textbf{H}=\frac{I\rm{d}\textbf{s} \times \textbf{e}_{r}}{4\pi r^{2}}\]と表される.

磁束密度 $B$ と磁界 $H$ との関係は,\[B=\mu_{0}H\]であることから,ビオ・サバールの法則の法則は,\[\rm{d}\textbf{B}=\frac{\mu_{0}I\rm{d}\textbf{s} \times \textbf{e}_{r}}{4\pi r^{2}}\]とも表される.

なお,点Pの磁界の向きはアンペアの右ねじの法則に従う.

Mathematics is the language with which God has written the universe.

無限長直線導体の周囲に生じる磁界 - ビオ・サバールの法則 - 補角の公式 - フレミングの左手の法則 - ローレンツ力