フレミングの左手の法則[Fleming’s left-hand rule]
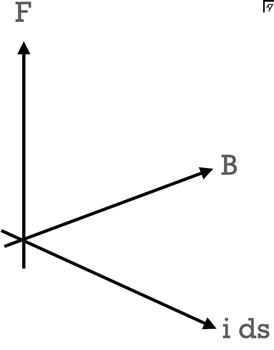
導線の断面積を $S$,導線内の自由電子の密度[単位体積あたりの数]を $n$,荷電粒子の平均速度を $v$ とすると,導線を流れる電流 $I$ は,\[I = n (−e) Sv\]と表すことができる.
これをフレミングの左手の法則の式に代入すると,\[d\textbf{F} = I \rm{ds} \times \textbf{B}=n (−e) Sv \cdot \rm{ds} \times \textbf{B}\]となる.
ここで, $n\rm{ds}$ は導線の長さ $\rm{ds}$ の部分に含まれる荷電粒子の数である.従って,1個の荷電粒子に着目し,かつ,1個の荷電粒子に働く力のベクトルを $\textbf{v}=v\rm{ds}$ とすると,\[\rm{F} = −e \textbf{v} \times \textbf{B}\]となり,この式において電荷 $-e$ を $q$ とおくと,ローレンツ力*の式となる.

Mathematics is the language with which God has written the universe.