定義:ベルヌーイ数[Bernoulli number]
ベルヌーイ数は関・ベルヌーイ数ともいう.これは,関孝和[/1708-12-05]がベルヌーイ[Jakob Bernoulli:1654-12-27/1705-08-16]とほぼ同時期にベルヌーイ数を発見していたことによる.
import Pkg
Pkg.add("Plots")
using Plots
#The Akiyama–Tanigawa algorithm
#以下の計算はThe-Bernoulli-Manifestoに基づく.
#http://luschny.de/math/zeta/The-Bernoulli-Manifesto.html
function bernoulli(n)
A = Vector{Rational{BigInt}}(undef, n + 1)
for m = 0 : n
# "//" は有理数表現.1//(m+1)は1/(m+1)のまま.
# m=0 のときは A[1]=1/(0+1)=1
# m=1 のときは A[2]=1/(1+1)=1/2
A[m + 1] = 1 // (m + 1)
# j を m から始めて 1 づつ 1 になるまで減らしていく.
# m=0 のときは j も 0 なので計算範囲外.
# m=1 のときは j も 1.A[1]-A[2]
for j = m : -1 : 1
A[j] = j * (A[j] - A[j + 1])
#A[j] = (-1)^j *j* (A[j] - A[j + 1])
end
end
return A[1]
end
# map 関数は配列の各値に対して関数を適用し,その結果を新しい配列として返す
x=0:1:15
B = map(bernoulli, x)
#ベルヌーイ数を描画
plot(x,B,labels=nothing,lw=4)
#グラフに水平線を入れる
hline!([0]; label="", color=:black)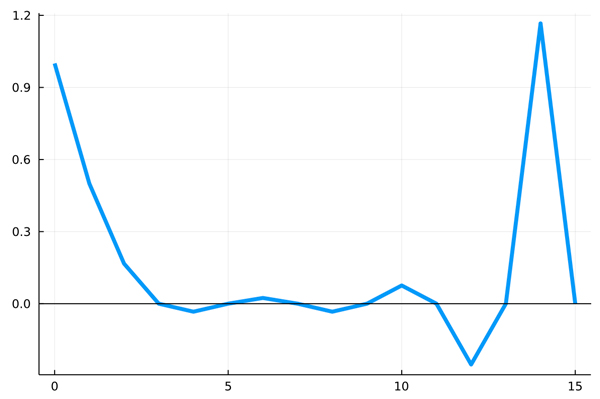

Mathematics is the language with which God has written the universe.