三相交流

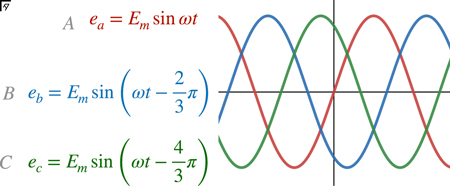
交流電力システムは,イタリアの物理学者・電気工学者であるガリレオ・フェラリス[Galileo Ferraris;1847-10-31/1897-02-07],ロシアのドブロヴォルスキー[Михаи́л О́сипович Доли́во-Доброво́льский;1862-01-02/1919-11-15],スウェーデンのウェンストロム[Jonas Wenström ;1855-08-04/1893-12-22],米国のニコラ・テスラ[Nikola Tesla;1856-07-10/1943-01-07]らによって1880年代末に発明.

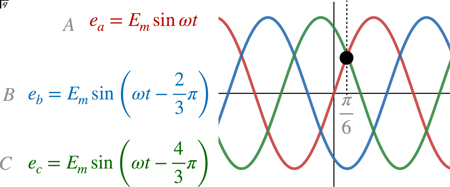
変圧器二次側の星形結線の各層にサイリスタを接続した三相半波整流回路においては,Bの電圧がAの電圧を上回ってから制御角 $\alpha$ でターンオンさせる.Bの電圧がAの電圧を上回るのは,\[\sin\left(\omega t\right)=\sin\left(\omega t-\frac{2}{3}\pi\right)\]となるとき,すなわち,\[\sin\left(\omega t\right)-\sin\left(\omega t-\frac{2}{3}\pi\right)=0\]となるときである.

ここで,\[\omega t-\frac{2}{3}\pi=x\]とおくと,\[\sin\left(\omega t\right)-\sin\left(\omega t-\frac{2}{3}\pi\right)=\sin\left(x+\frac{2}{3}\pi\right) - \sin x\]となる.

加法定理を用いると上式は,\[\sin\left(x+\frac{2}{3}\pi\right) - \sin x=\sin\left(x+\frac{1}{2}\frac{2}{3}\pi+\frac{1}{2}\frac{2}{3}\pi\right) - \sin\left(x+\frac{1}{2}\frac{2}{3}\pi-\frac{1}{2}\frac{2}{3}\pi\right)\]となり,\[\begin{eqnarray}\sin\left(x+\frac{1}{2}\frac{2}{3}\pi\right)\cos\frac{1}{2}\frac{2}{3}\pi &+& \cos\left(x+\frac{1}{2}\frac{2}{3}\pi\right)\sin\frac{1}{2}\frac{2}{3}\pi\\&-& \sin\left(x+\frac{1}{2}\frac{2}{3}\pi\right)\cos\frac{1}{2}\frac{2}{3}\pi+\cos\left(x+\frac{1}{2}\frac{2}{3}\pi\right)\sin\frac{1}{2}\frac{2}{3}\pi\end{eqnarray}\]となる.

整理すると,\[2\cos\left(x+\frac{1}{2}\frac{2}{3}\pi \right)\sin\frac{1}{2}\frac{2}{3}\pi\]となる.\[\sin\frac{1}{2}\frac{2}{3}\pi \neq 0\]であるから,結局,\[2\cos\left(x+\frac{1}{2}\frac{2}{3}\pi \right)\sin\frac{1}{2}\frac{2}{3}\pi=0\]となるのは,\[\cos\left(x+\frac{1}{2}\frac{2}{3}\pi\right) =0\]となるときである.\[\cos\frac{\pi}{2}=0\]であるから,\[x+\frac{1}{2}\frac{2}{3}\pi =\frac{\pi}{2}\]であり,\[x=\frac{\pi}{2}-\frac{1}{2}\frac{2}{3}\pi=\frac{1}{6}\pi\]となる.

Mathematics is the language with which God has written the universe.