三相半波整流回路

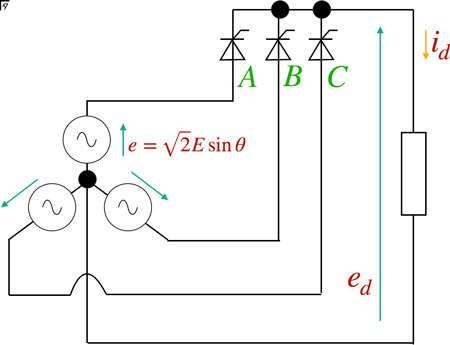
負荷の平均電圧を $E_{d}$ とすると,波形の周期は三相交流*の性質から $\frac{2}{3}\pi$,積分区間も同じく三相交流*の性質から,\[\frac{\pi}{6} +\alpha \sim \frac{5}{6}\pi+\alpha \]となることから,\[\begin{eqnarray}E_{d}&=&\frac{1}{\frac{2}{3}\pi}\int_{\frac{\pi}{6} +\alpha}^{\frac{5}{6}\pi+\alpha}\sqrt{2}E\sin\theta d \theta \\&=&\frac{3\sqrt{2}E}{2\pi}[-\cos\theta]_{\frac{\pi}{6} +\alpha}^{\frac{5}{6}\pi+\alpha}\\&=&\frac{3\sqrt{2}E}{2\pi}\left(-\cos\left(\frac{5}{6}\pi+\alpha \right)+\cos\left(\frac{\pi}{6} +\alpha \right) \right)\\&=&\frac{3\sqrt{2}E}{2\pi}\sin\left(\frac{\pi}{2}+\alpha \right)\sin\frac{\pi}{2}\\&=&\frac{3\sqrt{2}E}{2\pi}\cos\alpha\cdot\frac{\sqrt{3}}{2}\\&=&\frac{3\sqrt{6}E}{2\pi}\cos\alpha\\&=&1.17E\cos\alpha\end{eqnarray}\]となる.

Mathematics is the language with which God has written the universe.