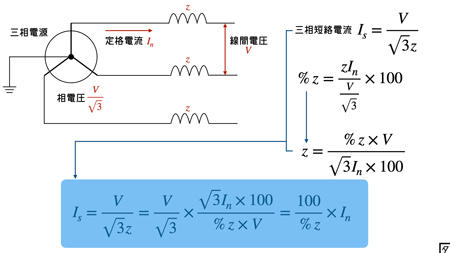
三相短絡電流
オームの法則である,\[I_{s}=\frac{E_{n}}{z}\]に対応している.
三相百分率インピーダンス,\[%z=\frac{zI_{n}}{V_{a}/\sqrt{3}}}[\textrm{\%}]\]を変形すると,\[\%z=\frac{\sqrt{3}zI_{n}}{V_{a}} \times 100\]となるから,ここから $z$ を求めると,\[z=\frac{\%z \times V_{a}}{\sqrt{3}I_{n} \times 100} \quad [\textrm{\Omega}]\]となる.
ここで,\[I_{s}=\frac{V_{1}}{\sqrt{3}z}\]であるから,これを先の式の $z$ に代入すると,\[I_{s}=\frac{V_{a}}{\sqrt{3}} \times \frac{\sqrt{3}I_{n} \times 100}{\%z \times V_{a}}=\frac{100}{\%z} \times I_{n} \quad [\textrm{A}]\]となる.
三相短絡電流

Mathematics is the language with which God has written the universe.