Point
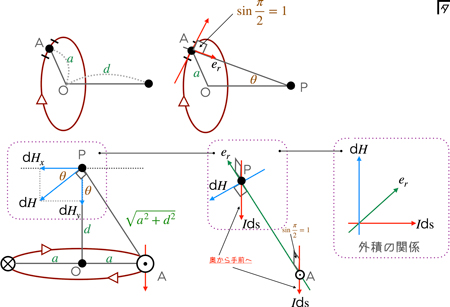
半径 $a$ の円形の導体に電流が流れるときにおける,中心点 $O$ から距離 $d$ だけ離れた点 $P$ に生じる磁界をビオ・サバールの法則*を用いて考える.電流素片 $I\textrm{d}l$ が点 $P$ に作る磁界の大きさは,\[\textrm{d}H=\frac{I\textrm{d}l}{4 \pi (a^{2}+d^{2})}\]となる.ここで,この磁界 $\textrm{d}H$ の水平成分と垂直成分を考える.水平成分は円形の導体における対照点において方向が逆となるため,\[\int\textrm{d}H_{x}=0\]となる.
垂直成分は,\[\textrm{d}H_{y}=\frac{I\textrm{d}l}{4 \pi (a^{2}+d^{2})}\cdot\frac{a}{\sqrt{a^{2}+d^{2}}}=\frac{aI\textrm{d}l}{4 \pi (a^{2}+d^{2})^{\frac{3}{2}}}\]従って,円形の導体を流れる電流全体が点 $P$ に作る磁界の大きさ $H$ は,\[H=\int\textrm{d}H_{y}=\int_{0}^{2 \pi a}\frac{aI\textrm{d}l}{4 \pi (a^{2}+d^{2})^{\frac{3}{2}}}=\frac{a^{2}I}{2(a^{2}+d^{2})^{\frac{3}{2}}} \]である.
なお,半径 $a$ の円形の導体の中心点 $O$ における磁界の大きさは $d=0$ を上式に代入することで,\[H_{O}=\frac{I}{2a}\]となる.

Mathematics is the language with which God has written the universe.