定義:判別式[discriminant]
2次方程式 \[ax^{2}+bx+c=0\]の解は,判別式を $D$ とすると,解の公式により,\[x=\frac{-b\pm\sqrt{D}}{2a}\]となる.
以上より,
例えば,\[2x^{2}+3x-10=0\]の場合は判別式が,\[D=b^{2}-4ac=3^{2}+4*2*10=9+80>0\]となるので異なる実数解を2つ持つ.
import Pkg; Pkg.add("Plots")
using Plots
f(x) = 2x^2+3*x-10
x=-20:0.1:20
y=f.(x) #関数fをxに適用
trim(f) = x -> f(x) > 700 ? NaN : f(x)
plot(x,y,label ="",linewidth=4,xlim = (-30,30))
#グラフに水平線・垂直線を入れる
hline!([0]; label="", color=:black)
vline!([0]; label="", color=:black)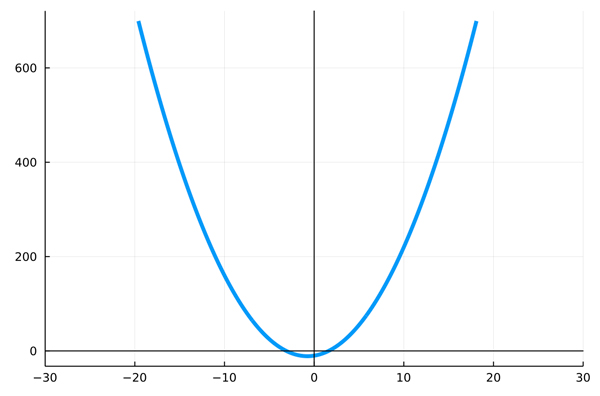
JuliaからPyPlotを呼び出して描画する場合.
import Pkg;
Pkg.add("PyCall");
using PyCall
@pyimport matplotlib.pyplot as plt
@pyimport numpy as np
x=-20:0.01:20
f(x) = 2x^2+3*x-10
x=-20:0.1:20
y=f.(x) #関数fをxに適用
plt.plot(x,y)
plt.legend()
plt.show()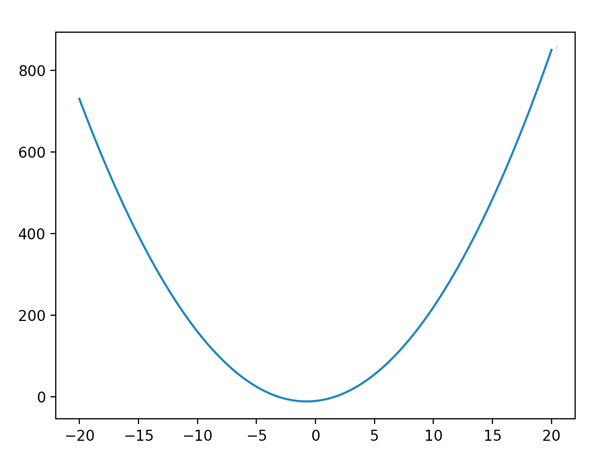

Mathematics is the language with which God has written the universe.