単相半波整流回路

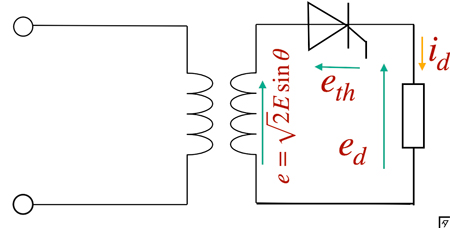
負荷の平均電圧を $E_{d}$ とすると,純負荷抵抗の場合は,\[\begin{eqnarray}E_{d}&=&\frac{1}{2\pi}\int_{\alpha}^{\pi}\sqrt{2}E\sin\theta d \theta\\&=&\frac{\sqrt{2}E}{2\pi}\int_{\alpha}^{\pi}\sin\theta d \theta\\&=&\frac{\sqrt{2}E}{2\pi}[-\cos \theta]_{\alpha}^{\pi}\\&=&\frac{\sqrt{2}E}{2\pi}\left(-\cos\pi-(-\cos\alpha) \right)\\&=&\frac{\sqrt{2}E}{2\pi}(1+\cos\alpha) \end{eqnarray}\]さらに計算すると,\[E_{d}=0.45E\frac{1+\cos\alpha}{2}\quad[\textrm{V}]\]

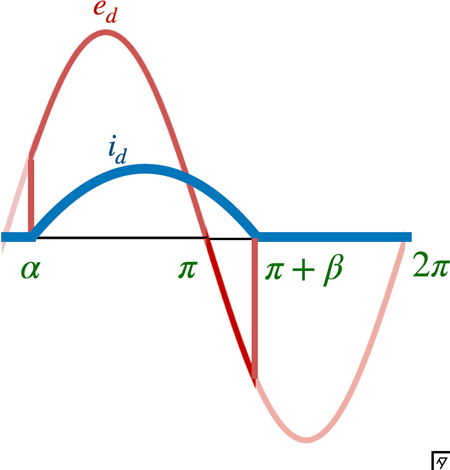
誘導性負荷の場合はインダクタンスの逆起電力によって電源電圧が $0$ になっても暫くは電流が流れる.下図でいうと,純負荷抵抗の場合は $\beta=0$であり,誘導性負荷の場合は $\beta \neq 0$ となる.

Mathematics is the language with which God has written the universe.