定義:双曲線正接関数[hyperbolic tangent]
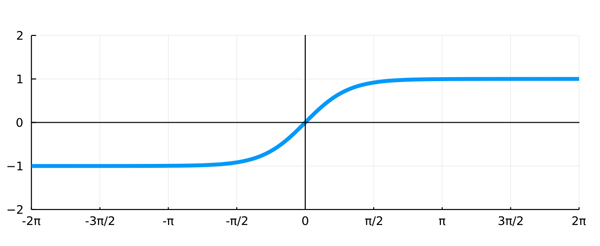
双曲線正接関数は座標点$(0, 0)$を基点[変曲点]として点対称となるS字型の滑らかな曲線であり,機械学習においてはシグモイド関数を拡張するという位置付けで活性化関数として用いられる.
using Plots #x軸の目盛に π を使うための設定. xticks_values = [-2π,-3π/2,-π,-π/2,0,π/2,π,3π/2,2π] xticks_labels = ["-2π","-3π/2","-π","-π/2","0","π/2","π","3π/2","2π"] plot(tanh,label=nothing,xticks = (xticks_values,xticks_labels),aspect_ratio=1,xlim=(-2π,2π),ylim=(-2,2),lw=4) #グラフに水平線を入れる hline!([0]; label="", color=:black) #グラフに垂直線を入れる vline!([0]; label="", color=:black)

Mathematics is the language with which God has written the universe.