$y$ は $u$ の線形関数であるので正規分布に従います.
従って,\[\begin{array}\ E(y)&=X\beta\\var(y)&=E(y-X\beta)(y-X\beta)'=E(uu')=\sigma^{2}I\end{array}\]となるので,\[y \sim N(X\beta,\sigma^{2}I)\]が成り立ちます.
よって,$y$ の尤度関数は,\[L=(2\pi\sigma^{2})^{-\frac{n}{2}}exp\{-\frac{1}{2\sigma^{2}}(y-X\beta)'(y-X\beta)\}\]となります.
対数尤度関数は,\[\log L=-\frac{n}{2}\log 2\pi-\frac{n}{2}\log\sigma^{2}-\frac{1}{2\sigma^{2}}(y-X\beta)'(y-X\beta)\]この対数尤度関数を $\beta$ に関して最大化することで最尤推定量(Maximum Likelihood Estimates;MLE)を得ることが出来ます.
つまり,\[\frac{\partial \log L}{\partial \beta}=-\frac{1}{2\sigma^{2}}\frac{{\partial }}{{\partial \beta}}(y'y-2y'X\beta+\beta'X'X\beta)\]を変形して,\[\frac{\partial \log L}{\partial \beta}=\frac{1}{2\sigma^{2}}(X'y-X'X\beta)=0\]となるので,\[\tilde{\beta}=(X'X)^{-1}X'y\]が最尤推定量(Maximum Likelihood Estimates;MLE)となります.
なお,ここで,\[\frac{{\partial \beta'x}}{{\partial x}}=\frac{{\partial x'\beta}}{{\partial x}}=\beta\]という行列の微分の公式を利用しています.
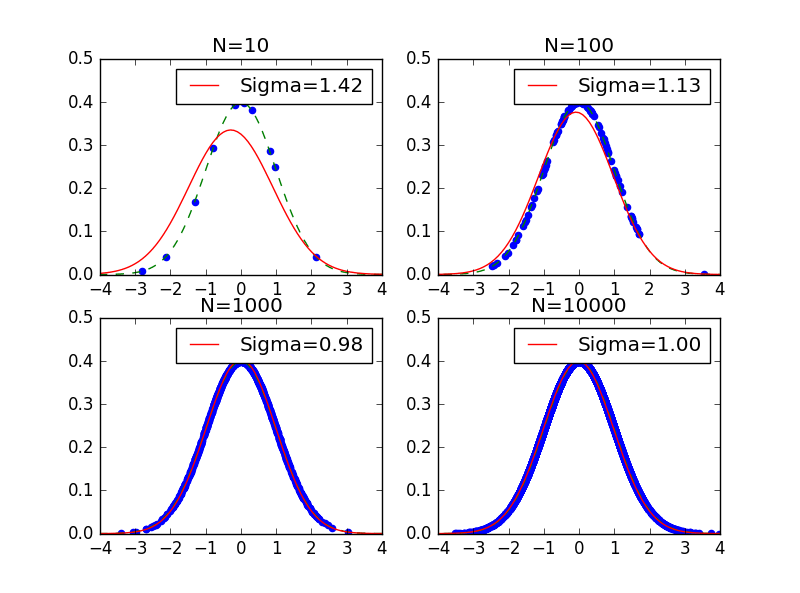
データ数が,10,100,1000,10000の場合の平均0,標準偏差1の正規分布の最尤推定量の値を Python で描いてみたのが以下の図になります.破線が実際の正規分布で,青い点が観測された値,赤い実線が観測された値から推定されたグラフになります.
データ数が増えるに従って,赤い実線が青い破線に一致していく様子がよく分かります.

Mathematics is the language with which God has written the universe.