変圧器の誘導電圧
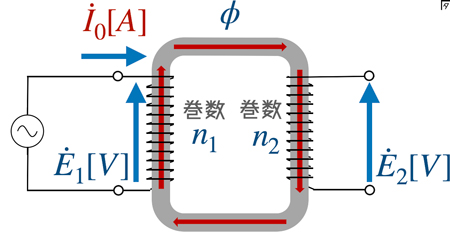
ファラデーの法則より,\[E_{1}'=-n_{1}\frac{\Delta \phi}{\Delta t}\]となることから,\[\phi=-\int \frac{E_{1}}{n_{1}}\textrm{dt}\]ここで,正弦波交流であることを考慮し,$E_{1}'$ の最大値を $E_{m}$ とすると,\[E_{1}'=E_{m}\sin \omega t\textrm{dt}\]であることを用いて,\[\begin{eqnarray}-\int \frac{E_{1}'}{n_{1}}\textrm{dt}&=&-\frac{E_{m}}{n_{1}}\int\sin \omega t\textrm{dt}\\&=&\frac{E_{m}}{n\omega}\cos \omega t \end{eqnarray}\]となる.
ここで,磁束 $\phi$ の最大値を $\phi_{m}$ とすると,\[\frac{E_{m}}{n\omega}\cos \omega t \equiv \phi_{m}\cos \omega t\]と定義する.
さらに,$E_{1}$ の平均値を $E_{avg}$ とすると最大値の $E_{m}$ との関係は,\[E_{avg}=E_{m} \times \left( \frac{2}{\pi} \right)\]となる.これを,先の磁束の最大値と誘導起電力との関係式に適用すると,\[E_{1}=n \cdot \omega \cdot \phi_{m} \cdot \left(\frac{2}{\pi}\right)\]となる.ここで,周波数を $f$ とすると,\[\omega=2 \pi f\]であるから,\[E_{1}=n \cdot (2\pi f) \cdot \phi_{m} \cdot \left(\frac{2}{\pi}\right)\]となり,結局,\[\omega=2 \pi f\]であるから,\[E_{avg}=n \cdot (2f) \cdot \phi_{m} \cdot 2=4 \cdot n \cdot f \cdot \phi_{m}\]となる.
電圧の実行値 $E_{RMS}$ は,\[E_{RMS}=\frac{E_{m}}{\sqrt{2}}\]という関係であるから,平均値 $E_{avg}$ との関係は,\[\frac{E_{RMS}}{E_{avg}}=\frac{E_{m}}{\sqrt{2}} \cdot \frac{1}{E_{m}}\frac{\pi}{2}=\frac{1}{\sqrt{2}} \cdot \sqrt{\pi}{2}=1.11\]となる.
以上より,\[E_{1}=4.44fn_{1}\phi_{m}\]となる$\square$

Mathematics is the language with which God has written the universe.