変圧器の負荷分担
単相変圧器の分担電流
容量の異なる変圧器 $A,B$ を並行運転するとき,一次換算したインピーダンスをそれぞれ $z_{a},z_{b}[\Omega]$ であり,変圧器 $A,B$ の抵抗とリアクタンスの比を等しいとすると,負荷電流 $I_{l}$[A] とそれぞれの変圧器分担電流 $I_{a},I_{b}$[A] の関係は,\[\begin{eqnarray}I_{a}&=&I_{l}\times\frac{z_{b}}{z_{a}+z_{b}}\\I_{b}&=&I_{l}\times\frac{z_{a}}{z_{a}+z_{b}} \end{eqnarray}\]となる.
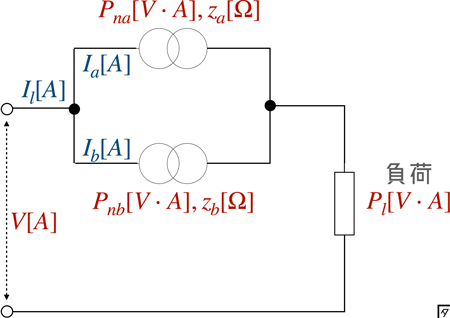
容量の異なる変圧器 $A,B$ を並行運転するとき,一次電圧・二次電圧が等しいとして等価回路を考えると以下の図のようになる.
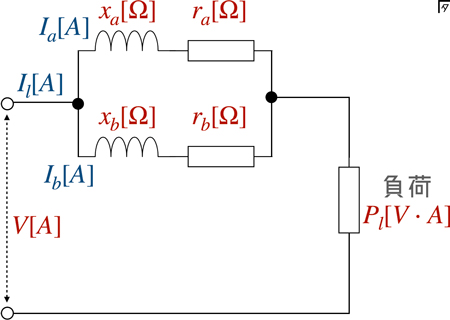
ここで,\[I_{a}=\frac{V}{z_{a}},I_{b}\frac{V}{z_{b}}\]であるから,\[V=\frac{I_{a}}{z_{a}}=\frac{I_{b}}{z_{b}}\]となる.
すなわち,\[\begin{eqnarray}I_{a}=\frac{z_{a}}{z_{b}}I_{b},I_{b}=\frac{z_{b}}{z_{a}}I_{a} \end{eqnarray}\]この式を先の式に代入すると,\[I_{a}+\frac{z_{a}}{z_{b}}I_{a}=I_{l}\]整理すると,\[\left(\frac{z_{a}+z_{b}}{z_{b}}\right)I_{a}=I_{l}\]さらに,\[I_{a}=I_{l}\times\frac{z_{b}}{z_{a}+z_{b}}\]となる.
$I_{b}$ についても同様に導くことができる.
単相変圧器の負荷分担
容量の異なる変圧器 $A,B$ を並行運転するとき,変圧器 $A$ の定格容量・分担負荷を $P_{na},P_{a}$ ,変圧器 $B$ の定格容量・分担負荷を $P_{nb},P_{b}$ とし,$\%z_{b}'$ を $\%z_{b}$ を変圧器 $A$ の定格容量 $P_{na}$ を基準容量として換算したものとすると,変圧器 $A$ と変圧器 $B$ の分担負荷は,\[\begin{eqnarray}P_{a}&=&P_{l} \times \frac{\%z_{b}'}{\%z_{a}+\%z_{b}'}\\P_{b}&=&P_{l} \times \frac{\%z_{a}}{\%z_{a}+\%z_{b}'} \end{eqnarray}\]となる.

Mathematics is the language with which God has written the universe.


