定義:平均値[average]
平均値は平均[mean],期待値[expectation]ともいわれる.
平均値は $\mu_{g(x)}$ と表す.
確率変数 $X$ が高々可算個 $(x_{1}, x_{2}, \cdots)$ を取るとき,すなわち,離散型確率変数であるとき,$X$ の平均値は,\[E(X)=\sum_{i=1}^{\infty}x_{i}p(X=x_{i})\]と表される.
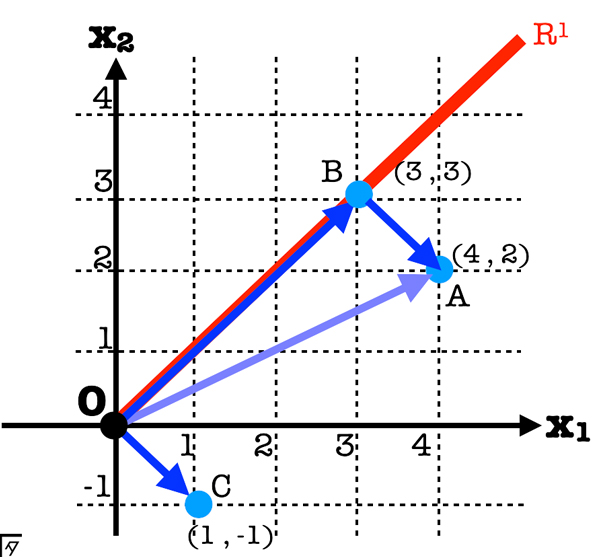
$X=(x_{1}, x_{2})=(4,2)$ のとき,平均は \[\mu=\frac{4+2}{2}=\frac{6}{2}=3\]となる.これを,$(x_{1}, x_{2})$ 平面上に表すと点Bとなる.つまり,平均値はベクトルOBで表される.ベクトルBAはデータ $X=(x_{1}, x_{2})=(4,2)$ と平均 $(3,3)$ との距離すなわち偏差 $(4-3,2-3)=(1,-1)$ となっている.図から分かるようにデータは平均と偏差に直交分解される.平均 $(3,3)$ と偏差 $(1,-1)$ が直交していることは,\[3 \cdot 1 + 3 \cdot (-1)=3-3=0\]となることからも確かめられる.
なお,母集団の平均のことは母平均[population mean]といい $\mu$ で表す.

Mathematics is the language with which God has written the universe.