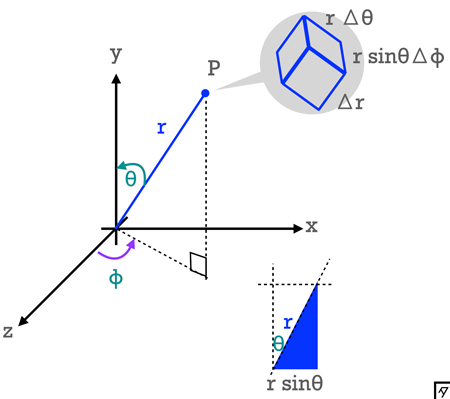
極座標[spherical polar coordinates]
$r$ は動径ともいわれ定義域は $0 \leq r \leq \infty$ ,$\theta$ は極角[天頂角]ともいわれ定義域は $0 \leq \theta \leq \pi$ ,$\phi$ は方位角[偏角]ともいわれ定義域は $0 \leq \phi \leq \pi$ である.
直交座標と極座標との関係は,\[\begin{eqnarray}x&=&r \sin \theta \cos \phi\\y&=&r \sin \theta \sin \phi \\z&=&r \cos \theta\end{eqnarray}\]と表される.
また,直交座標系で3次元の分布に関して積分を行う際は,\[\rm{d}x\rm{d}y\rm{d}x\]であるが,極座標系においては,\[r^{2}\sin\theta\rm{d}r\rm{d}\theta\rm{d}\phi\]で積分する.

Mathematics is the language with which God has written the universe.