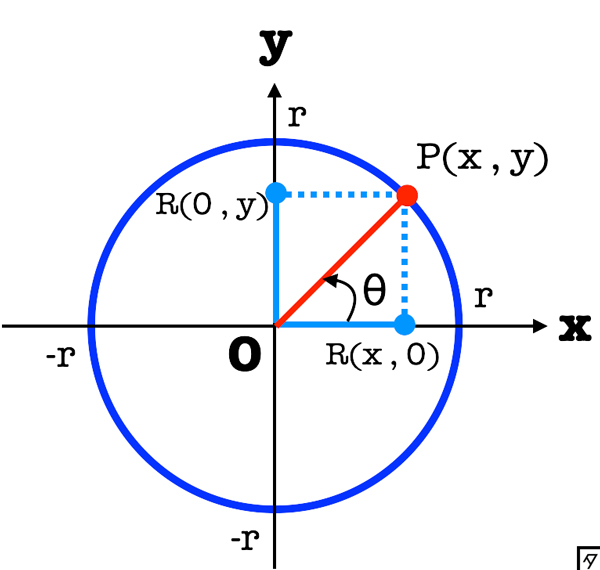
定義:正接関数[tangent function]
定義:正接関数[tangent function]
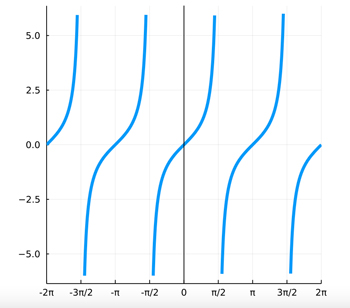
using Plots #x軸の目盛に π を使うための設定. xticks_values = [-2π,-3π/2,-π,-π/2,0,π/2,π,3π/2,2π] xticks_labels = ["-2π","-3π/2","-π","-π/2","0","π/2","π","3π/2","2π"] #-> は,引数 x を受け取って -> より右にある式に代入して返す #a ? b : cは,条件 a が真(true)なら b を,偽なら c を値とする3項演算子 #f(x) の絶対値が 6 よりも大きいときは NaNを,大きくないときは f(x) を返す trim(f) = x -> abs(f(x)) > 6 ? NaN : f(x) f(x)=tan(x) plot(trim(f),label=nothing,xticks = (xticks_values,xticks_labels),aspect_ratio=1,xlim=(-2π,2π),lw=4) #グラフに垂直線を入れる vline!([0]; label="", color=:black)

Mathematics is the language with which God has written the universe.