Point
点Aから点Bまでの長さが有限 $l_{1}+l_{2}$ である直線状の導線に電流 $I$ が流れている場合に,点 $O$ から距離 $d$ だけ離れている点 $P$ における磁界を求める.
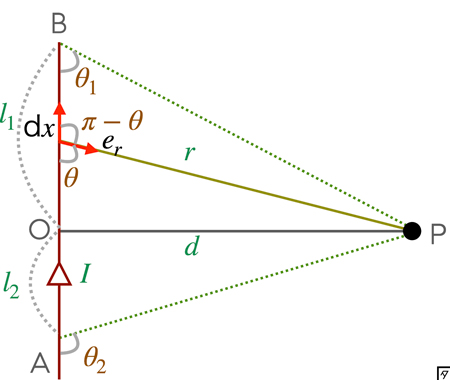
ビオ・サバールの法則*より,\[\textrm{d}\dot{H}=\frac{I\rm{d}x \times e_{r}}{4 \pi r^{2}}=\frac{I \sin(\pi - \theta)}{4 \pi r^{2}}\textrm{d}x\]となる.ここで,補角の公式*より,\[\sin(\pi - \theta)=\sin(\theta)\]であることを用いて,\[\textrm{d}\dot{H}=\frac{I \sin(\pi - \theta)}{4 \pi r^{2}}\textrm{d}x=\frac{I \sin(\theta)}{4 \pi r^{2}}\textrm{d}x=\frac{I \sin\theta}{4 \pi r^{2}}\textrm{d}x\]となる.
以上から,点Aから点Bまでの全ての電流素片 $\textrm{d}\dot{H}$ により点Pに作られる磁界の総和は,\[H=\int \textrm{d}\dot{H}=\int^{l_{1}}_{l_{2}}\frac{I \sin\theta}{4 \pi r^{2}}\textrm{d}x\]と表すことができる.
さらに,上図より,\[r=\frac{d}{\sin \theta},\tan \theta=\frac{d}{x}\]であるので,\[x=\frac{d}{\tan \theta}\]と表すことができる.ここで,\[\begin{eqnarray}\left(\frac{1}{\tan x} \right)'&=&\left(\frac{\cos x}{\sin x} \right)\\&=&\frac{(\cos x)'\sin x - (\sin x)'\cos x}{\sin^{2} x}\\&=&\frac{-\sin^{2}x - \cos^{2}x}{\sin^{2}x}\\&=&-\frac{1}{\sin^{2} x} \end{eqnarray}\]であることから,\[\frac{\textrm{d}x}{\rm{d}\theta}=-\frac{d}{\sin^{2}\theta}\]となるので,\[\textrm{d}x=-\frac{d}{\sin^{2}\theta}\textrm{d}\theta\]とおくことができる.
これを $\textrm{d}\dot{H}$ の式に代入すると,\[\textrm{d}\dot{H}=\frac{I \sin\theta}{4 \pi r^{2}}\textrm{d}=\frac{I \sin\theta}{4 \pi}\left(\frac{\sin \theta}{d}\right)^{2}\left(-\frac{d}{\sin^{2}\theta}\right)\textrm{d}\theta=-\frac{I \sin \theta}{4 \pi d}\textrm{d}\theta\]以上より,点Pに作られる磁界の総和は,\[\begin{eqnarray}H=\int^{l_{1}}_{l_{2}}\frac{I \sin\theta}{4 \pi r^{2}}\textrm{d}x&=&-\int^{\theta_{1}}_{\theta_{2}}\frac{I \sin\theta}{4 \pi d}\textrm{d}\theta\\&=&-\frac{I}{4 \pi d}[-\cos \theta]^{\theta_{1}}_{\theta_{2}}\\&=&\frac{I}{4 \pi d}(\cos \theta_{1} - \cos \theta_{2})\end{eqnarray}\]となる.
ここで,\[\cos \theta_{1}=\frac{l_{1}}{\sqrt{l_{1}^{2}+d^{2}}},\cos \theta_{2}=\frac{-l_{2}}{\sqrt{l_{2}^{2}+d^{2}}}\]であるので,これを代入すると,\[H=\frac{I}{4 \pi d}(\cos \theta_{1} - \cos \theta_{2})=\frac{I}{4 \pi d}\left(\frac{l_{1}}{\sqrt{l_{1}^{2}+d^{2}}}+\frac{l_{2}}{\sqrt{l_{2}^{2}+d^{2}}} \right)\]となる.
有限長の直線電流の場合の磁界の大きさを表す,\[H=\frac{I}{4 \pi d}\left(\frac{l_{1}}{\sqrt{l_{1}^{2}+d^{2}}}+\frac{l_{2}}{\sqrt{l_{2}^{2}+d^{2}}} \right)\]において,\[l_{1},l_{2} \longrightarrow \infty\]とすると,無限長直線導体の周囲に生じる磁界 $H$ の大きさが求まる.
すなわち,\[H=\frac{I}{4 \pi d}(1+1)=\frac{I}{2 \pi d}\]

Mathematics is the language with which God has written the universe.