球の表面積
球の断面図において,$x$ 軸から $\theta$ だけ傾けた直線と,そこからさらに $\Delta\theta$ だけ傾けた2本の直線を考える.そして,円と傾き $\theta$ の交点から球に沿って円を描く.こうして描かれる円の半径は $r \cos\theta$ ,円周の長さは $2 \pi r \cos\theta$ となる.
同様にして, $\theta+\Delta\theta$ の交点から球に沿って円を描く.こうして描かれる2つの円の間の幅は $r \Delta\theta$ となる.従って,2つの円に囲まれた面の面積は,\[S=2 \pi r \cos\theta r \Delta\theta\]
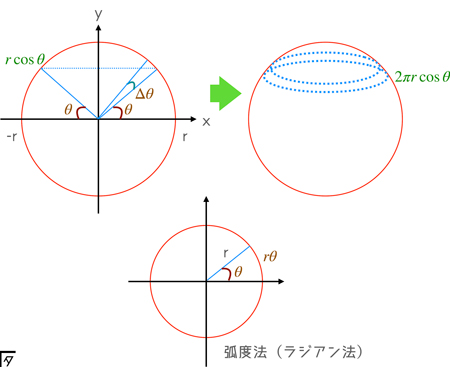
ここで,$\Delta\theta \longrightarrow 0$ として積分すると球の表面積を求めることができる.
すなわち,\[\begin{eqnarray}S&=&\int^{\frac{\pi}{2}}_{-\frac{\pi}{2}}2 \pi r \cos\theta r \textrm{d}\theta\\&=&\int^{\frac{\pi}{2}}_{-\frac{\pi}{2}}2 \pi r^{2} \cos\theta\textrm{d}\theta\\&=&2 \pi r^{2} \int^{\frac{\pi}{2}}_{-\frac{\pi}{2}}\cos\theta\textrm{d}\theta\\&=&2 \pi r^{2}[\sin\theta]^{\frac{\pi}{2}}_{-\frac{\pi}{2}}\\&=&2 \pi r^{2}{1-(-1)}\\&=&4 \pi r^{2} \end{eqnarray}\]
電磁気学において,球形が関係する式に $4\pi$[球因子:spherical factor]が,円筒形が関係する式には $2\pi$ が表れ,平板が関係する式には $\pi$ が表れないようにすることを,有理化された[rationalized]という.この球因子 $4\pi$ は,球の表面積,\[4 \pi r^{2}\]に由来する.SI単位系の一部であるMSKAは有利化された有理系であるため,電磁場を記述する電磁気学の基本方程式であるマクスウェル方程式では $4\pi$ は表れない.

Mathematics is the language with which God has written the universe.