補角の公式

補角の公式[supplementary angle formula]

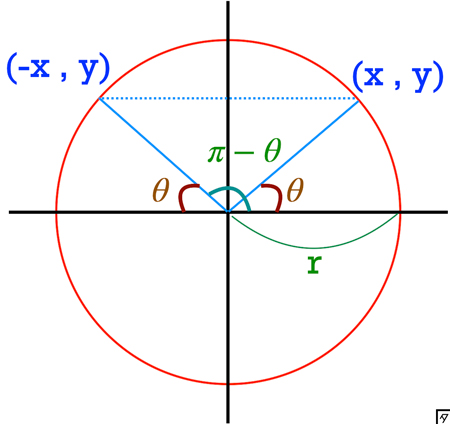
\[\begin{eqnarray}\sin(\pi - \theta)&=&\sin\theta\\ \cos(\pi - \theta)&=&-\cos\theta\\ \tan(\pi - \theta)&=&-\tan\theta \end{eqnarray}\]

$\theta$ のときの座標を $(x,y)$ とすると,\[\cos \theta=x , \sin \theta\]となる.

ここで,$\cos(\pi - \theta)$ のときの座標は対称性から $(-x,y)$ となる.

従って,\[\begin{eqnarray}\sin(\pi - \theta)&=&x\\ \cos(\pi - \theta)&=&-y\end{eqnarray}\]となる.

よって,\[\begin{eqnarray}\sin(\pi - \theta)&=&x=\sin \theta\\ \cos(\pi - \theta)&=&-y=-\cos \theta\end{eqnarray}\]となる.

また,\[\tan(\pi - \theta)=\frac{\sin(\pi - \theta)}{\cos(\pi - \theta)}=\frac{\sin \theta}{-\cos \theta}=-\tan \theta\]となる.

Mathematics is the language with which God has written the universe.