Point
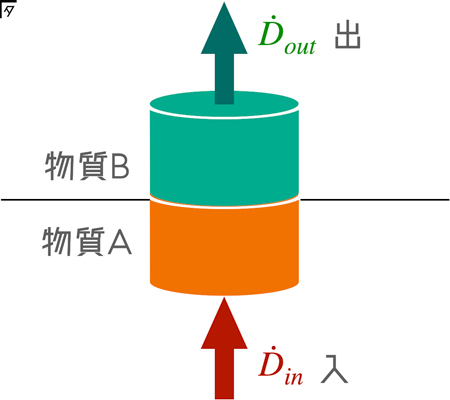
上図のように異なる誘電率をもつ物質の境界をまたがるような底面積 $S$ の微小円筒を考える.この微小円筒の底面から電束密度が出入りしている.ここで,閉曲面 $S$ の表面における電界を $\dot{E}$,面素ベクトルを $\textrm{d}\dot{S}$として,ガウスの法則の積分形を考える.閉曲面に対して,入る量と出る量が同じなので面積分の結果は $0$ となるので, \[\int_{S}\dot{D}(\dot{r},t) \cdot \textrm{d}\dot{S}\]となる.
すなわち,閉曲面に入ってくる電束密度を $\dot{D}_{in}$,出ていく電束密度を $\dot{D}_{out}$ とすると,その合計が $0$ となる.\[\dot{D}_{in} - \dot{D}_{out} = 0\]となる.この式を変形すると,\[\dot{D}_{in} = \dot{D}_{out}\]となる.これは,誘電体の境界を越えたといっても,境界面に対して垂直に入ってきた電束密度が不連続的に変化することはないということを意味している.

Mathematics is the language with which God has written the universe.