送受電端における電力
送受電端における電力
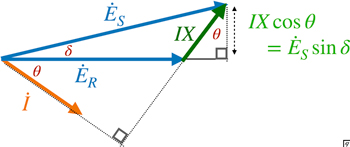
送電端相電圧を $V_{S}$[V] ,受電端相電圧を $V_{R}$[V] ,送電端相電圧と受電端相電圧との相差角を $\delta$ ,線路のリアクタンスを $X[\Omega]$ とし,線路に抵抗はないものとすると経路損失はないため,1相当たりの送電端電力と受電端電力は等しくなる.
この電力は, \[\begin{eqnarray}P&=&E_{R}I\cos\theta\\&=&\frac{E_{S}E_{R}}{X}\sin\delta\quad[\textrm{V}]\end{eqnarray}\]となる.
\[IX\cos\theta=E_{S}\sin\delta\]であることを用いて,\[E_{R}I\cos\theta=\frac{E_{R}}{X}IX\cos\theta\]と変形すると,\[\frac{E_{S}E_{R}}{X}\sin\delta\]を導くことができる.

Mathematics is the language with which God has written the universe.

