高木関数

定義：高木関数[Takagi function]

$s(x)$ を\[s(x)=\min_{n \in \mathbb{Z}}|x - n|\]によって定義される三角波関数[triangle function]とする.
このとき,単位区間$\lbrack0,1\rbrack$ 上において,\[T(x)=\sum_{n=0}^{\infty}\frac{s(2^{n}x)}{2^{n}}\]として定義される関数.

高木貞治[1875-04-21/1960-02-28]が1903年の論文において,「連続だが至る所で微分不可能な関数」として構成した関数.

y=$T(x)$ は周期1の周期関数である.

つまり,\[T(x+1)=T(x) , (\infty < x < \infty)\]が成り立つ.

プログラミング例[Julia 1.7]

import Pkg
Pkg.add("Plots")
using Plots

#三角波関数
s(x) = abs(x - round(x))

#struct は Fortranにおける構造体.
#変更不可能なものはstruct.変更が可能なものはmutable struct.
#名前と<:と既存の型を続けると,新しく宣言した型はその型を「親」とする
#サブタイプであることを指定
struct TakagiFunction{T<:Integer} <: Function
    #::演算子はプログラム中の式や変数に型注釈をつけるために使う
    #左側の式の値は右側の型のインスタンス
    N::T
end

# ::Name を追加することで引数の型を宣言
(F::TakagiFunction)(x) = sum(n->(0.5)^n*s(2^n*x), 0:F.N)


F0 = TakagiFunction(10)
x = 0:0.01:1
plot(x, F0.(x),label=nothing)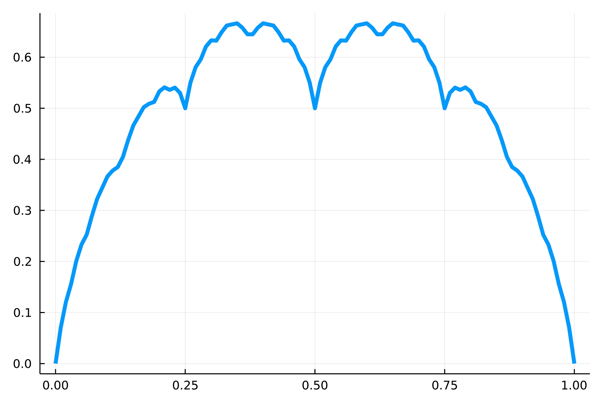

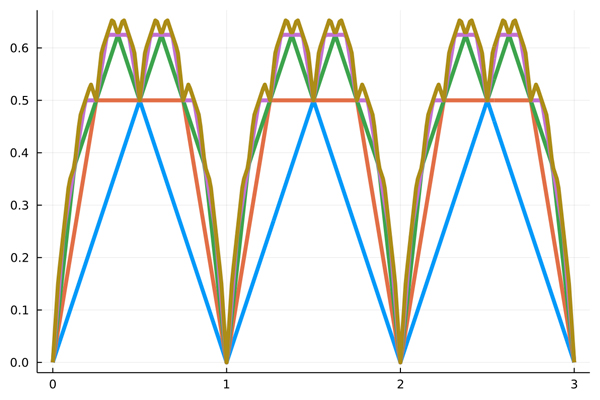
F0 = TakagiFunction(0)
x = 0:0.01:3
plot(x, F0.(x),label=nothing,lw=4)

F1 = TakagiFunction(1)
x = 0:0.01:3
#グラフを重ねて描画したい場合はplot!を使う
plot!(x, F1.(x),label=nothing,lw=4)

F2 = TakagiFunction(2)
x = 0:0.01:3
plot!(x, F2.(x),label=nothing,lw=4)

F3 = TakagiFunction(3)
x = 0:0.01:3
plot!(x, F3.(x),label=nothing,lw=4)

F4 = TakagiFunction(4)
x = 0:0.01:3
plot!(x, F4.(x),label=nothing,lw=4)

import Pkg
Pkg.add("Plots")
using Plots

#三角波関数
s(x) = abs(x - round(x))

#struct は Fortranにおける構造体.
#変更不可能なものはstruct.変更が可能なものはmutable struct.
#名前と<:と既存の型を続けると,新しく宣言した型はその型を「親」とする
#サブタイプであることを指定
struct TakagiFunction{T<:Integer} <: Function
    #::演算子はプログラム中の式や変数に型注釈をつけるために使う
    #左側の式の値は右側の型のインスタンス
    N::T
end


(F::TakagiFunction)(x) = sum(n->(0.5)^n*s(2^n*x), 0:F.N)


F0 = TakagiFunction(0)
x = 0:0.01:3
plt0=plot(x, F0.(x),label=nothing,lw=4,title ="N = $(F0.N+1)")

F1 = TakagiFunction(1)
x = 0:0.01:3
#グラフを重ねて描画したい場合はplot!を使う
plt1=plot(x, F1.(x),label=nothing,lw=4,title ="N = $(F1.N+1)")

F2 = TakagiFunction(2)
x = 0:0.01:3
plt2=plot(x, F2.(x),label=nothing,lw=4,title ="N = $(F2.N+1)")

F3 = TakagiFunction(3)
x = 0:0.01:3
plt3=plot(x, F3.(x),label=nothing,lw=4,title ="N = $(F3.N+1)")

F4 = TakagiFunction(4)
x = 0:0.01:3
plt4=plot(x, F4.(x),label=nothing,lw=4,title ="N = $(F4.N+1)")

F5 = TakagiFunction(5)
x = 0:0.01:3
plt5=plot(x, F5.(x),label=nothing,lw=4,title ="N = $(F5.N+1)")

plts=plot(plt0,plt1,plt2,plt3,plt4,plt5)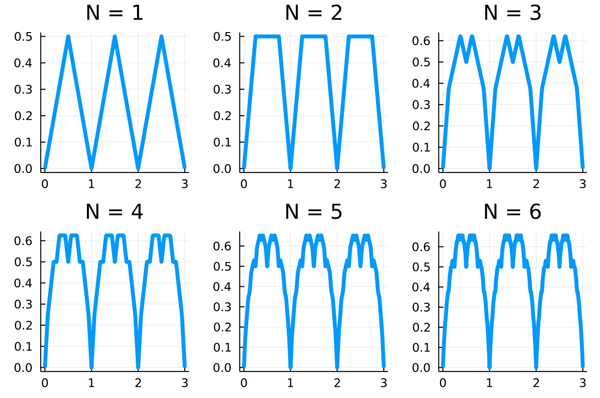

Mathematics is the language with which God has written the universe.

余割関数 - 高木関数 - ベルヌーイ数 - 判別式 - 正接関数