Y-Δ変換

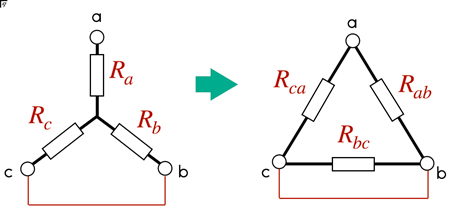
b-c間を短絡させて,Y回路におけるa-b間の合成コンダクタンスは,\[G_{Yab}=\frac{G_{ab}(G_{b}+G_{c})}{G_{a}+(G_{b}+G_{c})}\]同じく,a-b間におけるΔ回路の合成コンダクタンスは,\[G_{\Delta ab}=G_{ab}+R_{ca}\]となる.等価であるから両者は等しくなる.

c-a間を短絡させて,Y回路におけるa-b間の合成コンダクタンスは,\[G_{Ybc}=\frac{G_{b}(G_{c}+G_{a})}{G_{b}+(G_{c}+G_{a})}\]同じく,b-c間におけるΔ回路の合成コンダクタンスは,\[G_{\Delta bc}=G_{bc}+R_{ab}\]となる.等価であるから両者は等しくなる.

a-b間を短絡させて,Y回路におけるa-b間の合成コンダクタンスは,\[G_{Yca}=\frac{G_{c}(G_{a}+G_{b})}{G_{c}+(G_{a}+G_{b})}\]同じく,c-a間におけるΔ回路の合成コンダクタンスは,\[G_{\Delta ca}=G_{ca}+R_{bc}\]となる.等価であるから両者は等しくなる.

以上の関係式から,\[\begin{eqnarray}G_{ab}&=&\frac{G_{\Delta ab}+G_{\Delta bc}-G_{\Delta ca}}{2}\\&=&\frac{G_{Y ab}+G_{Y bc}-G_{Y ca}}{2}\\&=&\frac{G_{a}G_{b}}{G_{a}+G_{b}+G_{c}}\end{eqnarray}\]となる.

合成コンダクタンスの逆数をとると,\[\begin{eqnarray}\frac{1}{R_{ab}}&=&\frac{\frac{1}{R_{a}}\frac{1}{G_{b}}}{\frac{1}{G_{a}}+\frac{1}{G_{b}}+\frac{1}{G_{c}}}\\&=&\frac{\frac{1}{R_{a}R_{b}}}{\frac{R_{b}R_{c}+R_{a}R_{c}+R_{a}R_{b}}{R_{a}R_{b}R_{c}}}\\&=&\frac{R_{a}R_{b}R_{c}}{R_{b}R_{c}+R_{a}R_{c}+R_{a}R_{b}} \cdot \frac{1}{R_{a}R_{b}}\\&=&\frac{R_{b}R_{c}+R_{a}R_{c}+R_{a}R_{b}}{R_{c}}\end{eqnarray}\]

参照

• 直並列接続の合成抵抗

Mathematics is the language with which God has written the universe.