クーロンの法則

クーロンの法則に出てくる定数 $\varepsilon_{0}$ は真空の誘電率といい,\[\varepsilon_{0}=8.854 \times 10^{-12} [\rm{C^{2}/N \cdot m^{2}}] \]である.

力はベクトル量であることを考えると,$q_{1}$ から $q_{2}$ に向かうベクトル $\boldsymbol{r}$ を用いると,\[\boldsymbol{F_{1}}=-\boldsymbol{F_{2}}=-\frac{1}{4\pi\varepsilon_{0}} \cdot \frac{q_{1}q_{2}}{r^{2}} \cdot \frac{\boldsymbol{r}}{r}=-\frac{1}{4\pi\varepsilon_{0}} \cdot \frac{q_{1}q_{2}}{r^{2}}\boldsymbol{e} \]但し,$\boldsymbol{e}$ は $\boldsymbol{r}$ の単位ベクトルを表している.

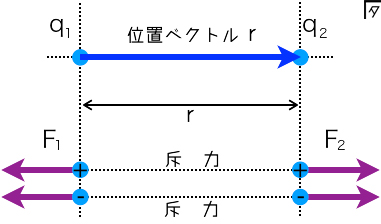
クーロンの法則の法則は,2点 $\boldsymbol{p}$,$\boldsymbol{q}$ に点電荷 $e_{1}$,$e_{1}$ があるとすると,それぞれの点電荷は,\[\frac{e_{1}e_{2}(\boldsymbol{p}-\boldsymbol{q})}{4\pi \varepsilon_{0}|\boldsymbol{p}-\boldsymbol{q}|^{3}} ,\frac{e_{1}e_{2}(\boldsymbol{q}-\boldsymbol{p})}{4\pi \varepsilon_{0}|\boldsymbol{q}-\boldsymbol{p}|^{3}}\]の力を受けると一般化することが出来る.

すなわち,電荷 $e_{1}$,$e_{1}$ を持つ質点は,その電荷が同符号であるときは斥ぞけ合い,異符号であるときは引き付け合う.そして,力の大きさは電荷の大きさの積に比例し,距離の2乗に反比例する.

INDEX