物体が円周上を一定の速さで回る運動を等速円運動という.
角速度[angular velocity]
ラジアン[rad,radian]
中心角が $\theta[rad]$ の円弧の長さ $l$ は,\[l=r \theta\]となる.
また,\[1\mathrm{\,[rad]} = \frac{360^{\circ}}{2\pi}\simeq57.3^{\circ}\]\[360^{\circ}=\frac{2\pi r}{r}=2\pi\mathrm{\,[rad]}\]である.
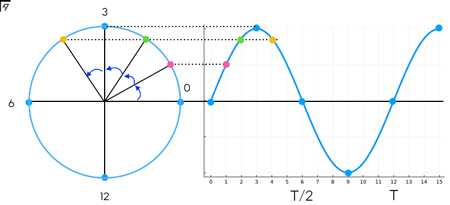
正弦波[sinusoidal wave]
円の半径を $A\mathrm{\,[m]}$,物体の速度を$v\mathrm{\,[m/s]}$,角速度を$A\mathrm{\,[rad/s]}$とする.このとき,1回転における移動距離は円周$2\pi A\mathrm{\,[m]}$,回転角は$2\pi\mathrm{\,[rad]}$であるから,周期$T\mathrm{\,[s]}$は,\[T=\frac{2\pi A}{v}=\frac{2\pi}{\omega}\]となる.
位相[phase]